Cho x+1/x=2 (x khác 0). Tính giá trị của A=x7+ 1/x7
Những câu hỏi liên quan
Cho biểu thức sau :B[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)a, Tìm giá trị của x để giá trị của biểu thức B được xác địnhb, Rút gọn Bc, Cmr với các giá trị của x mà giá trị của biểu thức xác định thì −5≤B≤0
Đọc tiếp
Cho biểu thức sau :
B=[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)[(x4−x+x−3x3+1).(x3−2x2+2x−1)(x+1)x9+x7−3x2−3+1−2(x+6)x2+1].4x2+4x+1(x+3)(4−x)a, Tìm giá trị của x để giá trị của biểu thức B được xác định
b, Rút gọn B
c, Cmr với các giá trị của x mà giá trị của biểu thức xác định thì −5≤B≤0
bài 4 : phân tích đa thức thành nhân tử rồi tính giá trị của các biểu thức sau :
a, A= 4(x - 2) (x+1) + (2x - 4)2 +(x+1)2 tại x = \(\dfrac{1}{2}\)
b, B= x9 - x7 - x6 - x5 + x4 + x3 + x2 - 1 tại x=1
a,
\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)
Thay $x=\dfrac12$ vào $A$, ta được:
\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)
Vậy $A=\dfrac94$ khi $x=\dfrac12$.
b,
\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)
Thay $x=1$ vào $B$, ta được:
\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)
Vậy $B=0$ khi $x=1$.
$Toru$
Đúng 1
Bình luận (0)
Tính giá trị của biểu thức:
-
x
7
y
5
z
2
:
-
x
y
3
z
2...
Đọc tiếp
Tính giá trị của biểu thức: - x 7 y 5 z 2 : - x y 3 z 2 tại x = 1; y = −10; z = 101
BT2: Thực Hiện các phép tính , sau đó tính giá trị biểu thức
a) A=(x-2).(x4+2x3+4x2+8x+16) Với x=3 ĐS A=211
b) B=(x+1).(x7-x6+x5-x4+x3-x2+x-1) Với x=2 ĐS B=255
a: A=x^5-32
Khi x=3 thì A=3^5-32=243-32=211
b: B=x^8-x^7+x^6-x^5+x^4-x^3+x^2-x+x^7-x^6+x^5-x^4+x^3-x^2+x-1
=x^8-1
=2^8-1=255
Đúng 0
Bình luận (0)
Giá trị của m để phương trình x 7 - x 2 = x - m có nghiệm x = 0 là?
A. m = 1
B. m = 0
C. m = ± 1
D. m = - 1
Bài 1: Cho hàm số f(x)x7 + 53sqrt[]{x^5+3cdot x^3+2}+12 Viết phương trình nhập vào 3 số thực a,b,c và đưa ra trung bình của f(a),f(b),f(c).Bài 2: Nhập x vào từ bàn phím và tính giá trị của biểu thức Adfrac{cos3a+^5sqrt{2X^3+x+1}}{log_7left(3^{x^2}+2.14bright)}trong đó asqrt{2^x+pi}và blnleft(e^{x+1.23}+1right)Lập trình ngôn ngữ C Em đang cần gấp ạ tại bài kiểm tra xin mn giúp đỡ
Đọc tiếp
Bài 1: Cho hàm số f(x)=x7 + 53\(\sqrt[]{x^5+3\cdot x^3+2}+12\) Viết phương trình nhập vào 3 số thực a,b,c và đưa ra trung bình của f(a),f(b),f(c).
Bài 2: Nhập x vào từ bàn phím và tính giá trị của biểu thức \(A=\dfrac{\cos3a+^5\sqrt{2X^3+x+1}}{\log_7\left(3^{x^2}+2.14b\right)}\)
trong đó \(a=\sqrt{2^x+\pi}\)
và \(b=\ln\left(e^{x+1.23}+1\right)\)
Lập trình ngôn ngữ C
Em đang cần gấp ạ tại bài kiểm tra xin mn giúp đỡ
Tính giá trị biểu thức :2 / 5 x7 + 2 /7 x 9 + 2 / 9 x 11 + ... + 2/13 x 15
\(\frac{2}{5\times7}+\frac{2}{7\times9}+\frac{2}{9\times11}+...+\frac{2}{13\times15}\)
\(=\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+...+\frac{1}{13}-\frac{1}{15}\)
\(=\frac{1}{5}-\frac{1}{15}\)
\(=\frac{2}{15}\)
Đúng 0
Bình luận (0)
= 2 x (1/ 5 x 7 + 1/ 7 x 9 + ... + 1/ 13 x 15)
= 2 x (1/5 - 1/7 + 1/7 - 1/9 + ... + 1/13 - 1/15)
= 2 x (1/5 - 1/15)
= 2 x (3/15 - 1/15)
= 2 x 2/15
= 4/15
Đúng 0
Bình luận (0)
Giá trị của đa thức x + x3 + x5 + x7 + x9 + ...... + x101 tại x = -1 là:
(A) -101;
(B) -100;
(C) -51;
(D) -50
Hãy chọn phương án đúng.
Thay x = -1 vào biểu thức đã cho ta được:
(-1) + ( -1)3 + (-1)5 + (-1)7 +...+ (-1)101
= (-1) + (-1) + (-1) + (-1) +(- 1)+ ... + (-1) (51 số -1)
= -51.
Chọn đáp án C
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
có đồ thị
f
(
x
)
như hình bên. Biết rằng:
f
(
x
3
)
f
(
x
o
)
và
f
(
x
1
)
+
f
(
x
2
)...
Đọc tiếp
Cho hàm số y = f ( x ) có đồ thị f ( x ) như hình bên. Biết rằng: f ( x 3 ) = f ( x o ) và f ( x 1 ) + f ( x 2 ) = f ( x 5 ) + f ( x 7 ) Giá trị lớn nhất của hàm số y = f ( x ) trên [ x 1 ; x 7 ] bằng
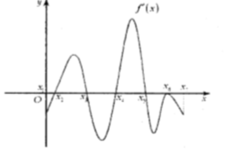
A . f ( x 1 )
B . f ( x 3 )
C . f ( x 5 )
D . f ( x 7 )
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
x
9
+
(
m
-
2
)
x
7
-
m
2
-
4
x
6
+
7
đạt cực tiểu tại x0? A. 3. B. 4. C. Vô số. D. 5.
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x 9 + ( m - 2 ) x 7 - m 2 - 4 x 6 + 7 đạt cực tiểu tại x=0?
A. 3.
B. 4.
C. Vô số.
D. 5.
Đáp án B
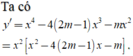
Dễ thấy x=0 là một nghiệm của đạo hàm y'. Do đó hàm số đạt cực tiểu tại x=0 khi và chỉ khi y'đổi dấu từ âm sang dương khi đi qua nghiệm x=0.Ta thấy dấu của y' là dấu của hàm số g ( x ) = x 2 - 4 2 m - 1 x - m . Hàm số g(x) đổi dấu khi đi qua giá trị x=0 khi x=0 là nghiệm của g(x). Khi đó g(0) = 0 ⇔ m=0
Thử lại, với m=0 thì g ( x ) = x 2 + 4 x đổi dấu từ âm sang dương khi đi qua giá trị x=0
Vậy có 1 giá trị m thỏa mãn yêu cầu bài toán
Đúng 0
Bình luận (0)