a) Thay m=3

\(x^2-2.3.m+3^2-3=0\)

\(x^2-6x+6=0\)

\(\text{∆}=6^2-4.6=12>0\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{6+\sqrt{12}}{2}=3+\sqrt{3}\\x=\dfrac{6-\sqrt{12}}{2}=3-\sqrt{3}\end{matrix}\right.\)

b) \(\text{∆}=\left(-2m\right)^2-4.\left(m^2-3\right)\)

\(=4m^2-4m^2+12=12>0\)

⇒ pt có 2 nghiệm phân biệt với mọi m

Câu a em tự giải nha.

b. \(\Delta'=\left(-m\right)^2-\left(m^2-3\right)\)

\(=m^2-m^2+3\)

\(=3>0\forall m\)

1) Thay m=1 vào phương trình, ta được:

\(x^2-2x+1=0\)

\(\Leftrightarrow\left(x-1\right)^2=0\)

\(\Leftrightarrow x-1=0\)

hay x=1

Vậy: Khi m=1 thì phương trình có nghiệm duy nhất là x=1

1) Bạn tự làm

2) Ta có: \(\Delta'=\left(m-1\right)^2\ge0\)

\(\Rightarrow\) Phương trình luôn có 2 nghiệm

Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m-1\end{matrix}\right.\) 

a) Ta có: \(x_1+x_2=-1\) \(\Rightarrow2m=-1\) \(\Leftrightarrow m=-\dfrac{1}{2}\)

   Vậy ...

b) Ta có: \(x_1^2+x_2^2=13\) \(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2=13\)

            \(\Rightarrow4m^2-4m-11=0\) \(\Leftrightarrow m=\dfrac{1\pm\sqrt{13}}{2}\)

  Vậy ... 

2) Ta có: \(\text{Δ}=\left(-2m\right)^2-4\cdot1\cdot\left(2m-1\right)=4m^2-8m+4=\left(2m-2\right)^2\ge0\forall m\)

Do đó, phương trình luôn có nghiệm với mọi m

Áp dụng hệ thức Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m}{1}=-2m\\x_1\cdot x_2=\dfrac{2m-1}{1}=2m-1\end{matrix}\right.\)

a) Ta có: \(x_1+x_2=-1\)

\(\Leftrightarrow-2m=-1\)

hay \(m=\dfrac{1}{2}\)

b) Ta có: \(x_1^2+x_2^2=13\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=13\)

\(\Leftrightarrow\left(-2m\right)^2-2\cdot\left(2m-1\right)=13\)

\(\Leftrightarrow4m^2-4m+2-13=0\)

\(\Leftrightarrow4m^2-4m+1-12=0\)

\(\Leftrightarrow\left(2m-1\right)^2=12\)

\(\Leftrightarrow\left[{}\begin{matrix}2m-1=2\sqrt{3}\\2m-1=-2\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\sqrt{3}+1\\2m=-2\sqrt{3}+1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{2\sqrt{3}+1}{2}\\m=\dfrac{-2\sqrt{3}+1}{2}\end{matrix}\right.\)

a, \(\Delta'=m^2-2m+1=\left(m-1\right)^2\)

Vậy pt luôn có 2 nghiệm 

b, để pt có 2 nghiệm pb khi m khác 1 

c, để pt có nghiệm kép khi m = 1 

d. Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2m\left(1\right)\\x_1x_2=2m-1\left(2\right)\end{matrix}\right.\)

Ta có \(x_1-2x_2=0\left(3\right)\)

Từ (1) ; (3) ta có \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1-2x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_2=2m\\x_1=2m-x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=2m-3\\x_1=2m-2m+3=3\end{matrix}\right.\)

Thay vào (2) ta được \(6m-9=2m-1\Leftrightarrow m=2\)

bài này sử dụng định lí vi-ét nha

1.Ta có \(\Delta=4m^2-4\left(m^2-m-3\right)=4m+12\)

Để phương trình có 2 nghiệm phân biệt \(\Rightarrow\Delta>0\Rightarrow4m+12>0\Rightarrow m>-3\)

Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m\\x_1.x_2=m^2-m-3\end{cases}}\)

a. Phương trình có 2 nghiệm trái dấu \(\Rightarrow x_1.x_2< 0\Rightarrow m^2-m-3< 0\Rightarrow\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)

Vậy \(\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)

b. Phương trình có 2 nghiệm phân biệt dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2=2m>0\\x_1.x_2=m^2-m-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}m>0\\m< \frac{1-\sqrt{13}}{2}\end{cases}\left(l\right);\hept{\begin{cases}m>0\\m>\frac{1+\sqrt{13}}{2}\end{cases}\Leftrightarrow m>\frac{1+\sqrt{13}}{2}}}}\)

Vậy \(m>\frac{1+\sqrt{13}}{2}\)

2. a.Ta có \(\Delta=\left(2m-1\right)^2+4m=4m^2-4m+1+4m=4m^2+1\)

Ta thấy \(\Delta=4m^2+1>0\forall m\)

Vậy phương trình luôn có 2 nghiejm phân biệt với mọi m

b. Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=1-2m\\x_1.x_2=-m\end{cases}}\)

Để \(x_1-x_2=1\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x2\right)^2-4x_1x_2=1\)

\(\Leftrightarrow\left(1-2m\right)^2-4.\left(-m\right)=1\Leftrightarrow4m^2-4m+1+4m=1\)

\(\Leftrightarrow m^2=0\Leftrightarrow m=0\)

Vậy \(m=0\)thoă mãn yêu cầu bài toán 

a: Khim=0 thì (1) trở thành \(x^2-2=0\)

hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)

Khi m=1 thì (1) trở thành \(x^2-2x=0\)

=>x=0 hoặc x=2

b: \(\text{Δ}=\left(-2m\right)^2-4\left(2m-2\right)\)

\(=4m^2-8m+8=4\left(m-1\right)^2>=0\)

Do đó: Phương trình luôn có hai nghiệm

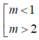
Chọn C

Đặt  t= x-1 hay x= t+1, thay vào pt đã cho ta được pt:

t²+ 2(1-m) t+ m²- 3 m+2= 0  (2)

pt (1) có 2 nghiệm thỏa  mãn x₁< 1< x₂ khi và chỉ khi  pt (2) có 2 nghiệm:  t₁< 0 < t₂  suy ra P < 0

Hay m²- 3m+ 2 < 0

Do đó:  1 <  m < 2

Kết luận: với 1< m< 2 thì pt (1) có hai nghiệm  x₁< 1< x₂