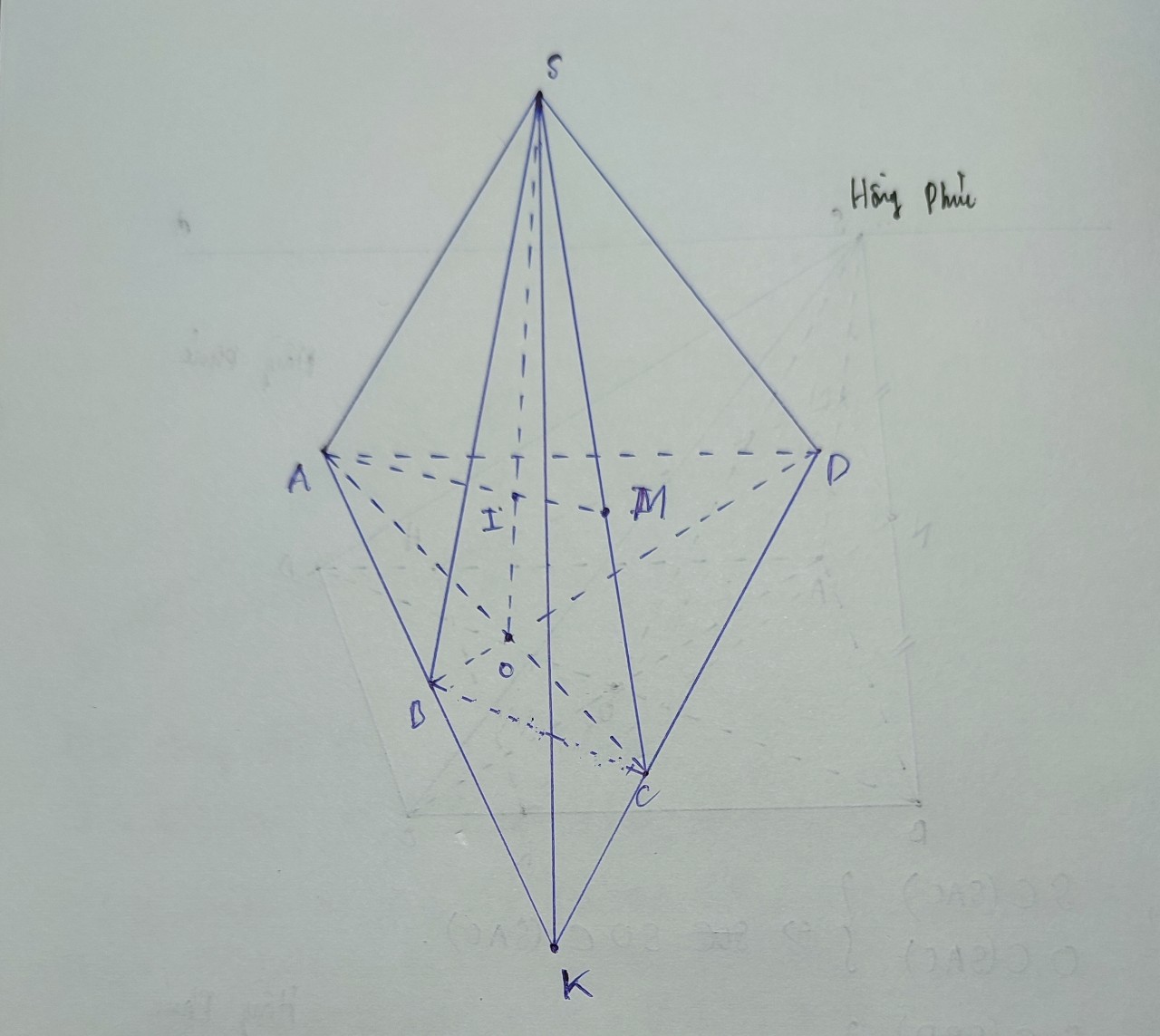
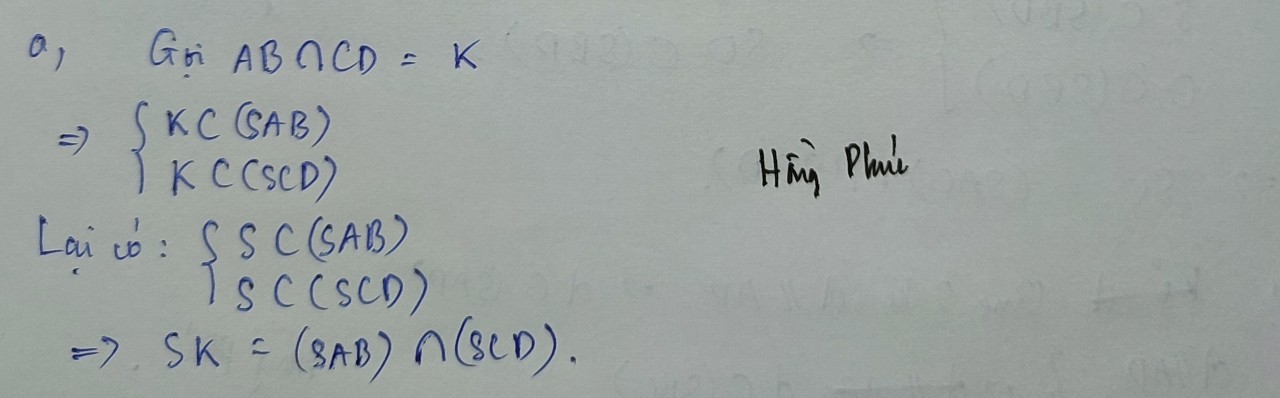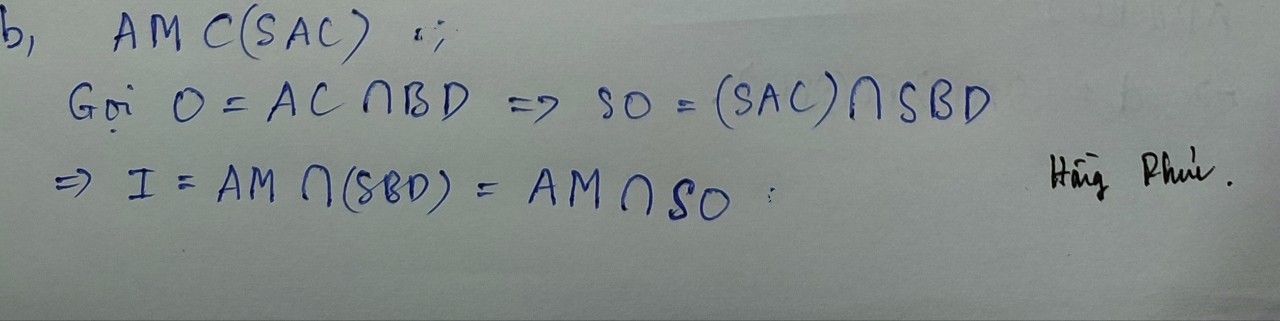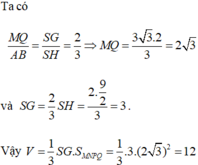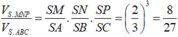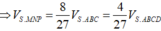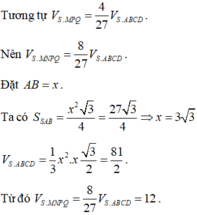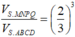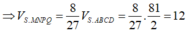cho hình chóp S.ABCD không có cạnh song song, M nằm trong miền tam giác SAB. CM: MC \(\cap\) (SBD).

Những câu hỏi liên quan
Cho hình chóp S.ABCD, ABCD là tứ giác không có cặp cạnh nào song song với nhau. Gọi M, N, K theo thứ tự là trung điểm của AB, AD, CD. I, J theo thứ tự là trọng tâm △SAB, △SAD.a)Tìm giao tuyến của các cặp mặt phẳng sau: (SAC)cap (SBD); (SAB) cap (SCD) và (SAD) cap (SBC)?b)Tìm giao điểm của đt MN và mặt phẳng (SAC)?c)Cmr: IJ//MN và MN//BD. Từ đó suy ra:IJ//(ABCD)d)Tìm giao tuyến của 2 mặt phẳng (IJK) và (ABCD)e)Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IJK)?
Đọc tiếp
Cho hình chóp S.ABCD, ABCD là tứ giác không có cặp cạnh nào song song với nhau. Gọi M, N, K theo thứ tự là trung điểm của AB, AD, CD. I, J theo thứ tự là trọng tâm △SAB, △SAD.
a)Tìm giao tuyến của các cặp mặt phẳng sau: (SAC)\(\cap\) (SBD); (SAB) \(\cap\) (SCD) và (SAD) \(\cap\) (SBC)?
b)Tìm giao điểm của đt MN và mặt phẳng (SAC)?
c)Cmr: IJ//MN và MN//BD. Từ đó suy ra:IJ//(ABCD)
d)Tìm giao tuyến của 2 mặt phẳng (IJK) và (ABCD)
e)Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IJK)?
a: Trong mp(ABCD), gọi X là giao điểm của AC và BD, Y là giao điểm của AB và CD; Z là giao điểm của AD và BC
X∈AC⊂(SAC)
X∈BD⊂(SBD)
Do đó: X∈(SAC) giao (SBD)(1)
S∈(SAC)
S∈(SBD)
Do đó: S∈(SAC) giao (SBD)(2)
Từ (1),(2) suy ra (SAC) giao (SBD)=SX
Y∈AB⊂(SAB)
Y∈CD⊂(SCD)
Do đó: Y∈(SAB) giao (SCD)(3)
S∈(SAB)
S∈(SCD)
Do đó: S∈(SAB) giao (SCD)(4)
Từ (3),(4) suy ra (SAB) giao (SCD)=SY
Z∈AD⊂(SAD)
Z∈BC⊂(SBC)
Do đó: Z∈(SAD) giao (SBC)(5)
S∈(SAD)
S∈(SBC)
Do đó: S∈(SAD) giao (SBC)(6)
Từ (5),(6) suy ra (SAD) giao (SBC)=SZ
b:
Chọn mp(ABD) có chứa MN
Xét (ABD) và (SAC) có
A∈(ABD) giao (SAC)
X∈(ABD) giao (SAC)
Do đó: (ABD) giao (SAC)=AX
Gọi T là giao điểm của MN và AX
=>T là giao điểm của MN và (SAC)
c: Xét ΔSAB có
SM là đường trung tuyến
I là trọng tâm
Do đó: S,I,M thẳng hàng và \(SI=\frac23SM\)
Xét ΔSAD có
N là trung điểm của AD
J là trọng tâm
Do đó: S,J,N thẳng hàng và \(SJ=\frac23SN\)
Xét ΔSMN có \(\frac{SI}{SM}=\frac{SJ}{SN}\left(=\frac23\right)\)
nên IJ//MN
Xét ΔABD có M,N lần lượt là trung điểm của AB,AD
=>MN là đường trung bình của ΔABD
=>MN//BD và \(MN=\frac{BD}{2}\)
MN//BD
JI//MN
Do đó: JI//BD
=>JI//(ABCD)
d: Xét (IJK) và (ABCD) có
K∈(IJK) giao (ABCD)
JI//BD
Do đó: (KIJ) giao (ABCD)=xy, xy đi qua K và xy//JI//BD
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác S.ABCD đáy tứ giác ABCD có AB không song song với CD,
gọi M là một điểm trên cạnh SC.
a) Tìm giao tuyến của (SAB) với (SCD).
b) Tìm giao điểm I của AM và (SBD)
giúp em với nhanh ạ:((
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi M là trung điểm của SC .Tính d(M,(SAB)) ; d(D,(SAC)) và (M,(SBD))
Cho hình chóp SABCD , đáy ABCD có các cặp cạnh đối không song song. Lấy M,N lần lượt nằm trên SA và SB sao cho MN không song song SB. G là trọng tâm ∆BCD. Xác định: a) Giao tuyến giữa (SAB) và (SDC), (MNC) và (SBD) b) Giao điểm CM với (SND), MG với (SBD) C) Thiết diện hình chóp khi cắt bởi mặt phẳng (MNG)
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB song song CD). Gọi G là trọng tâm của tam giác SCD. a) Tìm giao tuyến của hai mặt phẳng SCD và mặt phẳng GAB. b) Gọi M là điểm thuộc cạnh AC, sao cho AM = 2 MC. Chứng minh rằng MG song song (SAB) Giúp em bài này là cứu vớt con điểm Toán cuối kì đấy ạaaaaa :(((
a: \(G\in\left(SCD\right);G\in\left(GAB\right)\)
Do đó: \(G\in\left(SCD\right)\cap\left(GAB\right)\)
Xét (SCD) và (GAB) có
\(G\in\left(SCD\right)\cap\left(GAB\right)\)
CD//AB
Do đó: (SCD) giao (GAB)=xy, xy đi qua G và xy//AB//CD
Đúng 0
Bình luận (0)
cho hình chóp S.ABCD đáy ABCD là tứ giác lồi (các cặp cạnh đối không song song. Gọi F là điểm thuộc cạnh SB
a) tìm giao tuyến của 2 mặt phẳng (SAB) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SDF)
c) tìm giao tuyến của 2 mặt phẳng (FCD) và (SBC)
a: \(SB\subset\left(SAB\right)\)
\(SB\subset\left(SBD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SBD\right)=SB\)
b: \(F\in SB\subset\left(SAB\right);F\in\left(SDF\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(SDF\right)\)
mà \(S\in\left(SAB\right)\cap\left(SDF\right)\)
nên \(\left(SAB\right)\cap\left(SDF\right)=SF\)
c: \(F\in SB\subset\left(SBC\right);F\in\left(FCD\right)\)
\(\Leftrightarrow F\in\left(SBC\right)\cap\left(FCD\right)\)
mà \(C\in\left(CBS\right)\cap\left(FCD\right)\)
nên \(\left(FCD\right)\cap\left(SBC\right)=CF\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng
27
3
4
(đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S? A. V 24 B. V 8 C. V 12 D. V 36
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng 27 3 4 (đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S?
A. V = 24
B. V = 8
C. V = 12
D. V = 36
Đáp án là C
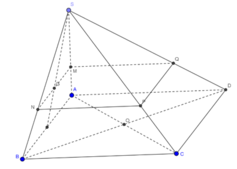
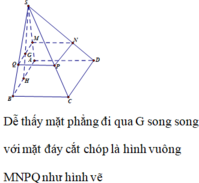
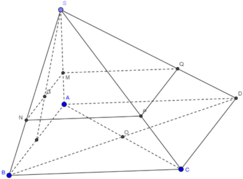
Cách 1. Ta có mặt phẳng (P) đi qua trọng tâm của tam giác SAB cắt các cạnh của khối chóp lần lượt tại M, N, P, Q. Với MN//AB, NP//BC, PQ//CD, QM//AD.
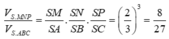
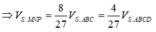
Tương tự 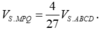
Nên 
Đặt AB = x.
Ta có 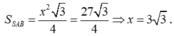
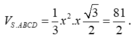
Từ đó 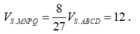
Cách 2. Do hai khối chóp S.MNPQ, S.ABCD đồng dạng với nhau theo tỉ số k = 2 3 nên tỉ lệ thể tích là
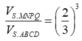
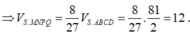
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng
27
3
4
(đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S? A. V 24 B. V 8 C. V 12 D. V 36
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng 27 3 4 (đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S?
A. V = 24
B. V = 8
C. V = 12
D. V = 36
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng
27
3
4
(đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S? A. V 24 B. V 8 C. V 12 D. V 36
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông, mặt bên (SAB) là một tam giác đều nằm trong mặt phẳng vuông góc với mặt đáy (ABCD) và có diện tích bằng 27 3 4 (đvdt). Một mặt phẳng đi qua trọng tâm tam giác SAB và song song với mặt đáy (ABCD) chia khối chóp S.ABCD thành hai phần, tính thể tích V của phần chứa điểm S?
A. V = 24
B. V = 8
C. V = 12
D. V = 36
Cho hình chóp S.ABCD có các cạnh AB và CD không song song ; O là giao điểm của hai đường thẳng AC và BD. Giao tuyến của các cặp mặt phẳng (SAC) và (SBD), (SAB) và (SCD) lần lượt là:
A. SA và SI, I là giao điểm của AB, CD
B. SO và SI, I là giao điểm của AB, CD
C. SB và SO
D. SD và SO