Những câu hỏi liên quan
giúp em câu này với ạ em cảm ơn nhiềuuuu
Giải giúp em câu 1, câu 2, câu 4 với ạ em cảm ơn
2.
Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=\sqrt{8^2+3^2-2.8.3.cos60^0}=7\)
\(S_{ABC}=\dfrac{1}{2}ac.sinB=\dfrac{1}{2}.8.3.sin60^0=6\sqrt{3}\)
4.
\(\Delta=\left(m+2\right)^2-16>0\Leftrightarrow m^2+4m-12>0\Rightarrow\left[{}\begin{matrix}m>2\\m< -6\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m-2\\x_1x_2=4\end{matrix}\right.\)
\(x_1+x_2+x_1x_2>1\)
\(\Leftrightarrow-m-2+4>1\)
\(\Rightarrow m< 1\) (2)
Kết hợp (1); (2) ta được \(m< -6\)
Đúng 0
Bình luận (0)
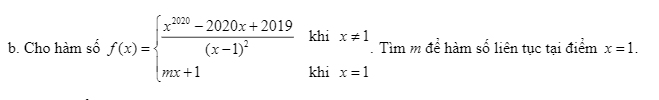
giúp em với em cảm ơn nhiềuuuu
Bài này xài L'Hopital đi, chứ tách biểu thức chắc đến sáng mai :D
\(\lim\limits_{x\rightarrow1}\dfrac{x^{2020}-2020x+2019}{\left(x-1\right)^2}=\lim\limits_{x\rightarrow1}\dfrac{2020x^{2019}-2020}{2\left(x-1\right)}=\lim\limits_{x\rightarrow1}\dfrac{2019.2020.x^{2018}}{2}=1010.2019\)
Hàm liên tục tại \(x=1\) khi: \(m+1=1010.2019\Rightarrow m=1010.2019-1\)
Đúng 2
Bình luận (0)
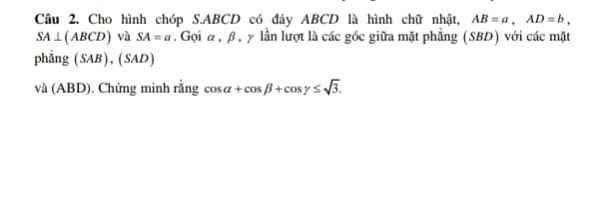
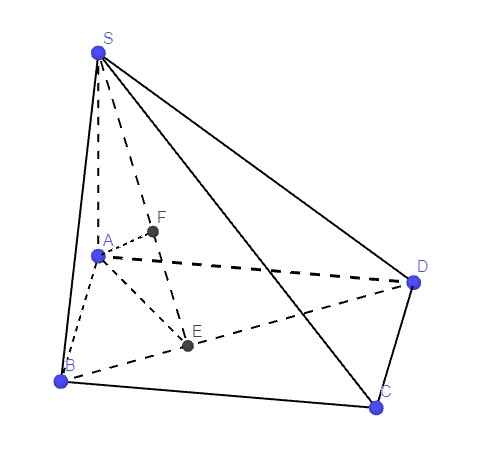
giúp em với em cảm ơn nhiềuuuu
Kẻ \(AE\perp BD\) , \(AF\perp SE\Rightarrow AF\perp\left(SBD\right)\)
Dễ dàng chứng minh \(AD\perp\left(SAB\right)\) ; \(AB\perp\left(SAD\right)\)
Từ đó ta có: \(\alpha=\widehat{FAD}\) ; \(\beta=\widehat{FAB}\) ; \(\gamma=\widehat{FAS}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}+\dfrac{1}{AD^2}=\dfrac{2}{a^2}+\dfrac{1}{b^2}=\dfrac{a^2+2b^2}{a^2b^2}\)
\(\Rightarrow AF=\dfrac{ab}{\sqrt{a^2+2b^2}}\)
\(\Rightarrow T=cos\alpha+cos\beta+cos\gamma=\dfrac{AF}{AD}+\dfrac{AF}{AB}+\dfrac{AF}{AS}=\dfrac{ab}{\sqrt{a^2+2b^2}}\left(\dfrac{2}{a}+\dfrac{1}{b}\right)\)
\(\Rightarrow T=\dfrac{\sqrt{3}ab}{\sqrt{\left(1+2\right)\left(a^2+2b^2\right)}}\left(\dfrac{a+2b}{ab}\right)\le\dfrac{\sqrt{3}ab}{a+2b}\left(\dfrac{a+2b}{ab}\right)=\sqrt{3}\)
Dấu "=" xảy ra khi và chỉ khi \(a=b\)
Đúng 1
Bình luận (0)

giúp em với ạ em cảm ơn nhiềuuuu
Xung quanh ô quân vua đang đứng có 8 ô, nên ở mỗi một bước, quân vua có 8 cách di chuyển
\(\Rightarrow\) Quân vua có \(8^3\) cách di chuyển 3 bước
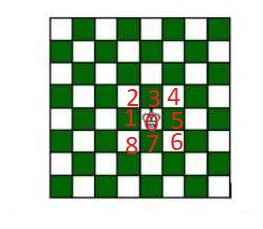
Ở bước đầu tiên, quân vua có 3 kiểu đi: sang các ô xanh hoặc sang các ô đỏ
TH1: quân vua sang ô xanh: có 4 cách. Do vai trò các ô như nhau, giả sử quân vua sang ô số 1
Để sau 2 bước nữa quay về ô 0 ban đầu, ở bước tiếp theo nó phải đi vào 1 ô nằm kế ô 0 \(\Rightarrow\) có 4 cách (là các ô 2,3,7,8)
Vậy có 4.4=16 cách
TH2: Quân vua sang ô trắng (có 4 cách) giả sử là ô số 2, vẫn như trên, bước thứ 2 nó phải sang 1 ô nằm kế ô số 0 => có 2 cách
\(\Rightarrow\) 4.2 =8 cách
Vậy quân vua có \(16+8=24\) cách đi thỏa mãn
Xác suất: \(\dfrac{24}{8^3}=...\)
Đúng 1
Bình luận (0)
giúp em giải câu 1 và 2 với ạ, em cảm ơn mọi người
Mọi người giúp e với giải giúp em câu 2 và câu 3 ạ em xin cảm ơn 

mn giải giúp em câu 1 đến câu 7 là chọn đáp án, câu 8 đến 10 giải cụ thể. em cảm ơn
Giải giúp em câu 2 được không ạ em xin cảm ơn
2a. Input: Số n: số lượng số của dãy số nguyên
n số nguyên từ \(n_0\) đến \(n_{n-1}\)
Output: Tổng các số chẵn trong dãy số nguyên từ \(n_0\) đến \(n_{n-1}\)
b. Input: Một số nguyên n
Output: In ra Yes nếu n là số nguyên tố, ngược lại in No.
c. Input: Nhập 3 số a, b, c bất kì
Output: Đưa ra kết quả các loại tam giác, nếu không là tam giác, in ra: "Không là 3 cạnh của một tam giác".
Đúng 0
Bình luận (0)
giải giúp em câu 2 cảm ơn nhìu 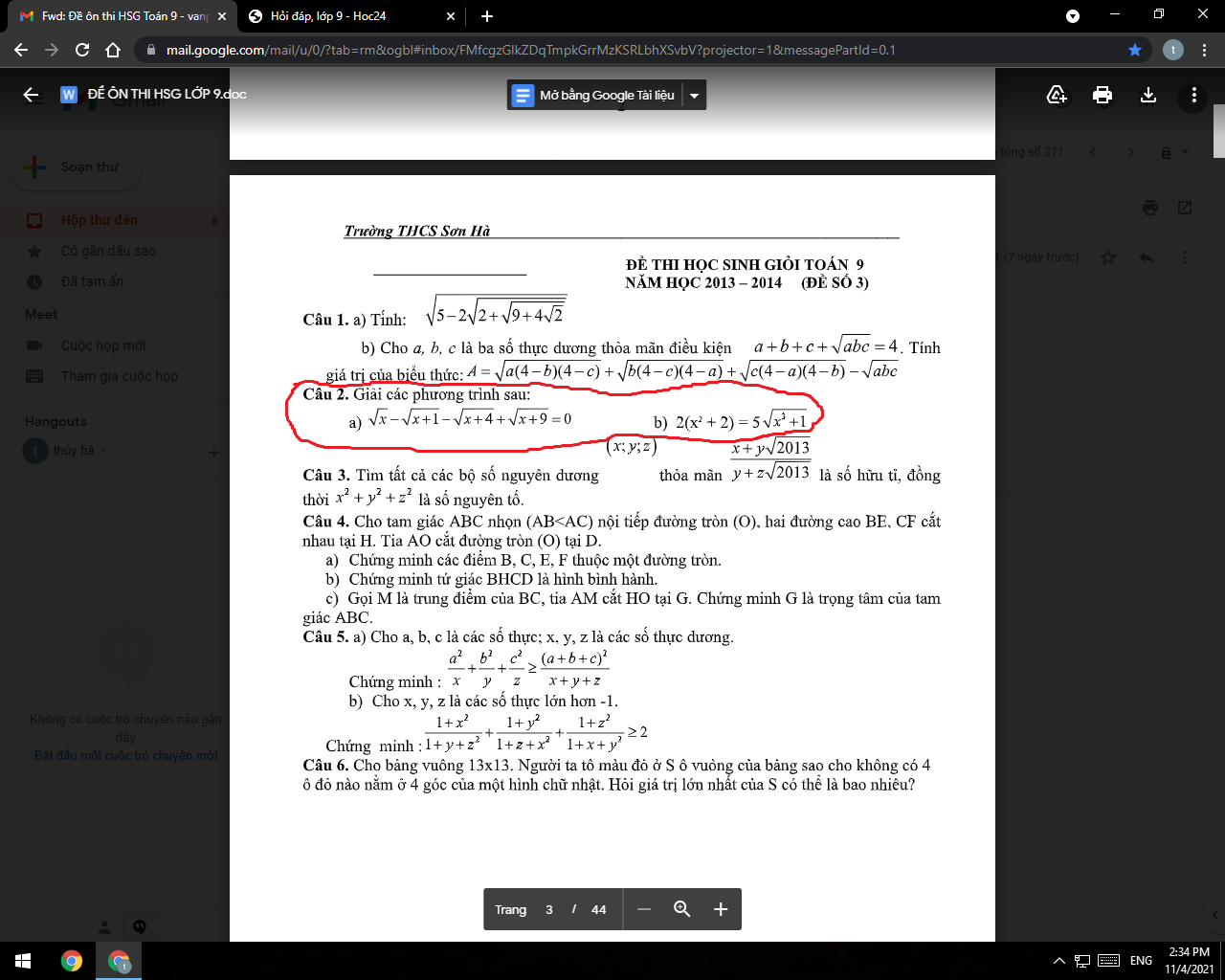
Câu 2:
\(a,ĐK:x\ge0\\ PT\Leftrightarrow\sqrt{x}-\left(\sqrt{x+1}-1\right)-\left(\sqrt{x+4}-2\right)+\left(\sqrt{x+9}-3\right)=0\\ \Leftrightarrow\sqrt{x}-\dfrac{x}{\sqrt{x+1}+1}-\dfrac{x}{\sqrt{x+4}+2}+\dfrac{x}{\sqrt{x+9}+3}=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}-\dfrac{\sqrt{x}}{\sqrt{x+1}+1}-\dfrac{\sqrt{x}}{\sqrt{x+4}+2}+\dfrac{\sqrt{x}}{\sqrt{x+9}+3}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\\sqrt{x}-\dfrac{\sqrt{x}}{\sqrt{x+1}+1}-\dfrac{\sqrt{x}}{\sqrt{x+4}+2}+\dfrac{\sqrt{x}}{\sqrt{x+9}+3}=0\left(1\right)\end{matrix}\right.\)
Với \(x\ge0\Leftrightarrow\left(1\right)>0\)
Vậy PT có nghiệm x=0
Đúng 0
Bình luận (0)
\(b,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\), PTTT:
\(2\left(a^2+b^2\right)=5ab\\ \Leftrightarrow2a^2-5ab+2b^2=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\\ \forall a=2b\Leftrightarrow x+1=4\left(x^2-x+1\right)\\ \Leftrightarrow4x^2-5x+3=0\\ \Delta=25-48< 0\\ \Leftrightarrow x\in\varnothing\\ \forall b=2a\Leftrightarrow x^2-x+1=4\left(x+1\right)\\ \Leftrightarrow x^2-5x-3=0\\ \Delta=25+12=37\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(n\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(n\right)\end{matrix}\right.\)
Vậy ...
Đúng 0
Bình luận (0)