Bài 4. Tìm giá trị nhỏ nhất của biểu thức:
M = 9x2 + 6y2 + 18x - 12xy - 12y -27.
Những câu hỏi liên quan
cho biểu thức:M=9x^2+6y^2+18x-12xy-12y-27. Khẳng định nào sau đây là đúng?a.M > 0 b.M<0 c.M>36 d.M<36
Cho x, y là hai số thực dương thỏa mãn điều kiện
4
+
9.3
x
2
−
2
y
4
+
9
x
2
−
2
y...
Đọc tiếp
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9.3 x 2 − 2 y = 4 + 9 x 2 − 2 y .7 2 y − x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
A. P = 3 + 2 2
B. P = 1 + 9 2
C. P = 9
D. Không tồn tại
Cho x, y là hai số thực dương thỏa mãn điều kiện
4
+
9
.
3
x
2
-
2
y
(
4
+
9
x
2
-
2
y
)
.
7
2...
Đọc tiếp
Cho x, y là hai số thực dương thỏa mãn điều kiện 4 + 9 . 3 x 2 - 2 y = ( 4 + 9 x 2 - 2 y ) . 7 2 y - x 2 + 2 .Tìm giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x .
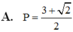
D. Không tồn tại
tìm giá trị nhỏ nhất của biểu thức: 9x2+12xy-12xz+6x+8y2+4yz+12y+17z2+4z+14
Cho x, y là hai số thực dương thỏa mãn
4
+
9.3
x
2
−
2
y
4
+
9
x
2
−
2
y
.7...
Đọc tiếp
Cho x, y là hai số thực dương thỏa mãn 4 + 9.3 x 2 − 2 y = 4 + 9 x 2 − 2 y .7 2 y − x 2 + 2 . Giá trị nhỏ nhất của biểu thức P = x + 2 y + 18 x bằng
A. 9
B. 3 + 2 2
C. 1 + 9 2
D. 17
Tìm GTNN:
M=9x^2+6y^2+18x-12xy-12y-27
GTNN của M là -36, đạt tại x = -1, y = 0. 🤡🤡
Đúng 0
Bình luận (0)
Tìm GTNN:
M=9x^2+6y^2+18x-12xy-12y-27
Biến đổi biểu thức \(M=9x^{2}+6y^{2}+18x-12xy-12y-27\) được biến đổi như sau: \(M=(9x^{2}-12xy+4y^{2})+(2y^{2}-12y+18)+(18x-36)-9\) \(M=(3x-2y)^{2}+2(y^{2}-6y+9)+18(x-2)-9\) \(M=(3x-2y)^{2}+2(y-3)^{2}+18(x-2)-9\) Để tìm giá trị nhỏ nhất, cần tìm mối liên hệ giữa \(x\) và \(y\). Đặt \(y-3=0\implies y=3\). Thay \(y=3\) vào biểu thức: \(M=(3x-2(3))^{2}+2(3-3)^{2}+18(x-2)-9\) \(M=(3x-6)^{2}+0+18(x-2)-9\) \(M=9(x-2)^{2}+18(x-2)-9\) Đặt \(t=x-2\). Biểu thức trở thành: \(M=9t^{2}+18t-9\) \(M=9(t^{2}+2t+1)-18\) \(M=9(t+1)^{2}-18\) Tìm giá trị nhỏ nhất Vì \((t+1)^{2}\ge 0\) với mọi \(t\), nên \(9(t+1)^{2}\ge 0\). Do đó, \(9(t+1)^{2}-18\ge -18\). Giá trị nhỏ nhất của \(M\) là \(-18\) khi \(t+1=0\implies t=-1\). Thay \(t=x-2\), ta có \(x-2=-1\implies x=1\). Thay \(x=1\) và \(y=3\) vào biểu thức ban đầu để kiểm tra: \(M=9(1)^{2}+6(3)^{2}+18(1)-12(1)(3)-12(3)-27\) \(M=9+54+18-36-36-27\) \(M=81-99=-18\). Kết luận Giá trị nhỏ nhất của biểu thức \(M\) là \(-18\).
Học tốt nha 👍
M=9x^2+6y^2+18x-12xy-12y-27
M=9x2+6y2+18x−12xy−12y−27
=(9x2−12xy+4y2)+( 18x−12y)+9+2y2−36
=[(3x)2 −2.3x.2y+(2y)2]+(18x−12y)+ 9+2y2− 36
=(3x−2y)2+2.(3x−2y) .3+32+2y2−36
=(3x−2y+3)2+2y2−36
∀x;y ta có :
(3x−2y+3)2≥0
2y2≥0
⇒(3x−2y+3)2+2y2≥0
⇒(3x-2y+3)2+2y2-36≥-36
⇒M≥-36
Dấu = xảy ra ⇔{3x−2y+3=02y2=0
⇔{x=-1 y=0
Vậy MinM=-36⇔{x=-1 y=0
Do đó : M≥−36
⇒ Chọn đáp án D
Đúng 1
Bình luận (0)
M=9x^2+6y^2+18x-12xy-12y-27
