chỉ ra các tia phân giác trong các hình vẽ sau
chỉ ra các tia phân giác trong các hình vẽ sau

Những câu hỏi liên quan
Bài 2. Cho AOB > 90 , vẽ các tia OM ⊥OB và ON ⊥OA . Vẽ tia Ox là phân giác của góc AOM , vẽ tia Oy⊥ Ox . Chỉ ra trong hình vẽ những cặp góc nhọn nào có cạnh tương ứng vuông góc với nhau.
Giải:
Các cặp góc nhọn có cạnh tương ứng vuông góc với nhau là:
\(\left(x\widehat{O}B;B\widehat{O}N\right);\left(A\widehat{O}y;y\widehat{O}M\right)\)
Đúng 0
Bình luận (0)
cho hình vẽ . Biết O1=O2 ;O3=O4 và hai tia ox ,On đối nhau . Chỉ ra các tia phân giác trên hình bên ; Tính số đo của góc moy
cho điểm O thuộc đường thẳng xy trên nửa mặt phẳng bờ xy vẽ hai tia Om ,On sao cho xOy bằng 70 độ ,xom bằng 40 độ a )Vẽ hình nêu tên các góc trong hình vẽb)chỉ ra các góc kề bù với xOm c)Tính yOm và mon d)tia On có phải là tia phân giác của moy khôngBài 2Cho xOy và yOz là hai góc kề bù biết xOy bằng 110 độa)Tính xOzb )Vẽ tia Om là tia phân giác của xOy on là tia phân giác của xOz tính monGiúp mk nha :333
Đọc tiếp
cho điểm O thuộc đường thẳng xy trên nửa mặt phẳng bờ xy vẽ hai tia Om ,On sao cho xOy bằng 70 độ ,xom bằng 40 độ
a )Vẽ hình nêu tên các góc trong hình vẽ
b)chỉ ra các góc kề bù với xOm
c)Tính yOm và mon
d)tia On có phải là tia phân giác của moy không
Bài 2
Cho xOy và yOz là hai góc kề bù biết xOy bằng 110 độ
a)Tính xOz
b )Vẽ tia Om là tia phân giác của xOy on là tia phân giác của xOz tính mon
Giúp mk nha :333
Bài 2:
a)
Sửa đề: Tính \(\widehat{yOz}\)
Ta có: \(\widehat{xOy}+\widehat{yOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{yOz}+110^0=180^0\)
hay \(\widehat{yOz}=70^0\)
b) Ta có: Om là tia phân giác của \(\widehat{xOy}\)
nên \(\widehat{xOm}=\dfrac{\widehat{xOy}}{2}=\dfrac{110^0}{2}=55^0\)
Ta có: \(\widehat{xOm}+\widehat{mOz}=180^0\)(hai góc kề bù)
nên \(\widehat{mOz}=180^0-\widehat{xOm}=180^0-55^0=125^0\)
Ta có: On là tia phân giác của \(\widehat{yOz}\)
nên \(\widehat{zOn}=\dfrac{\widehat{zOy}}{2}=\dfrac{70^0}{2}=35^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia Oz, ta có: \(\widehat{zOn}< \widehat{zOm}\left(35^0< 125^0\right)\)
nên tia On nằm giữa hai tia Oz và Om
\(\Leftrightarrow\widehat{zOn}+\widehat{mOn}=\widehat{zOm}\)
\(\Leftrightarrow35^0+\widehat{mOn}=125^0\)
hay \(\widehat{mOn}=90^0\)
Vậy: \(\widehat{mOn}=90^0\)
Đúng 0
Bình luận (0)
Cho hai đường thẳng xx’ và yy’ cắt nhau tại O và 0 xOy = 80 a) Vẽ hình và chỉ ra các góc kề bù với góc xOy, các cặp góc đối đỉnh có trong hình. b) Vẽ Ot là tia phân giác của x Oy ' ' . Tính số đo x Ot ' .
a: Các góc kề bù với góc xOy là \(\hat{xOy^{\prime}};\hat{x^{\prime}Oy}\)
Các cặp góc đối đỉnh là:
\(\hat{xOy^{\prime}};\hat{x^{\prime}Oy}\) ; \(\hat{xOy};\hat{x^{\prime}Oy^{\prime}}\)
b: Sửa đề: Tính số đo của \(\hat{x^{\prime}Ot}\)
Ta có: \(\hat{xOy^{\prime}}+\hat{xOy}=180^0\) (hai góc kề bù)
=>\(\hat{xOy^{\prime}}=180^0-80^0=100^0\)
Ot là phân giác của góc xOy'
=>\(\hat{xOt}=\frac{100^0}{2}=50^0\)
Ta có: \(\hat{xOt}+\hat{x^{\prime}Ot}=180^0\) (hai góc kề bù)
=>\(\hat{x^{\prime}Ot}=180^0-50^0=130^0\)
Đúng 0
Bình luận (0)
cho góc xOy bằng 120 độ . trên nửa mặt thẳng Ox chứa tia Oy vẽ hai tia Om và On sao cho góc xOm bằng 180 độ và góc mOn bằng 40 độ . a)Hãy chỉ ra các tia phân giác của góc có trong hình vẽ và chứng minh b)trên tia Oy lấy điểm A . vẽ tia At cắt các tia Om,On,Ox lần lượt tại các điểm B,C,D . Trên hình vẽ có bao nhiêu đoạn thẳng , bao nhiêu cặp góc kề bù
cho góc xOy bằng 120 độ . trên nửa mặt thẳng Ox chứa tia Oy vẽ hai tia Om và On sao cho góc xOm bằng 180 độ và góc mOn bằng 40 độ . a)Hãy chỉ ra các tia phân giác của góc có trong hình vẽ và chứng minh b)trên tia Oy lấy điểm A . vẽ tia At cắt các tia Om,On,Ox lần lượt tại các điểm B,C,D . Trên hình vẽ có bao nhiêu đoạn thẳng , bao nhiêu cặp góc kề bù
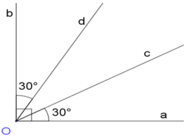
Cho a O b ^ = 90 0 . Bên trong a O b ^ vẽ các tia Oc tạo với Oa một góc 30 ° , tia Od tạo với Ob một góc 30 ° . Hãy chỉ ra những tia là tia phân giác.
cho góc xOy có số đo = 120 độ.trên cùng 1 nửa mặt phẳng bờ là dường thăng Ox chứa Oy vẽ 2 tia Om,On(ko trừng tia Ox,Oy)sao cho góc xOm =80 độ,mOn = 40 độ
a) hãy chỉ ra các tia phân giác của các góc trong hình vẽ và chứng minh
b)trên tia Oy lấy A vẽ tia AT cắt các tia Om,On,Õ lần lượt B,C,D.trên hình vẽ có bao nhiêu đoạn thẳng .có bao nhiêu góc kề bù
Cho tam giác ABC, tia phân giác của góc A cắt cạnh BC ở D. Từ D kẻ tia Dx // AB cắt cạnh AC ở E, vẽ tia Dy // AC cắt cạnh AB ở F .
a) Vẽ hình và ghi giả thiết kết luận
b) Tia DA có phải là tia phân giác của góc EDF không? Vì sao?
c) So sánh các góc của tam giác ABC và các góc của tam giác BDF
d) Chỉ ra các tam giác có hai góc bằng nhau
cùi . đéo giải được bài lớp 6 của tao.
Đúng 0
Bình luận (0)
mk chỉ bt vẽ hình thui cn c/m mk chưa hc đến phần này ms hc từ vuông góc đến song song thui thông cảm
Đúng 0
Bình luận (0)