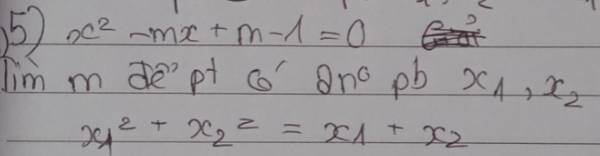
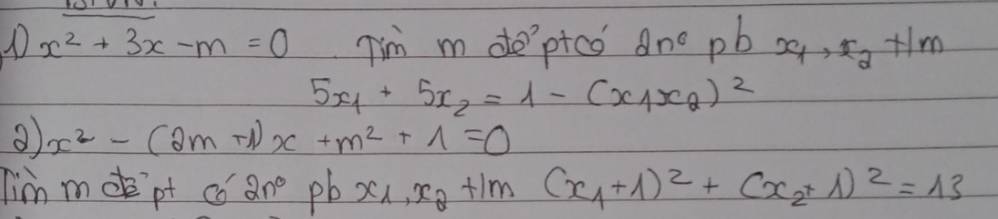
5.

\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)

Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)

Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)

\(x_1^2+x_2^2=x_1+x_2\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)

\(\Leftrightarrow m^2-2\left(m-1\right)=m\)

\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)

1.

\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)

\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)

\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)

\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)

\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)

2.

\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)

\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)

\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)

\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)

\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)

\(\Leftrightarrow2m^2+8m-10=0\)

\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)

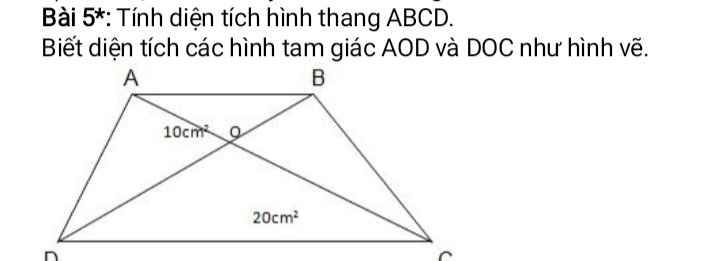
\(\dfrac{S_{AOD}}{S_{DOC}}=\dfrac{10}{20}=\dfrac{1}{2}\)

=>\(AO=\dfrac{1}{2}CO\)

Vì ABCD là hình thang có hai đáy là AB và CD

và AC cắt BD tại O

nên \(S_{AOD}=S_{BOC}\)

=>\(S_{BOC}=10\left(cm^2\right)\)

\(AO=\dfrac{1}{2}OC\)

=>\(S_{AOB}=\dfrac{1}{2}\cdot S_{BOC}=5\left(cm^2\right)\)

\(S_{ABCD}=S_{ABO}+S_{BOC}+S_{DOC}+S_{AOD}\)

\(=5+10+20+10=45\left(cm^2\right)\)

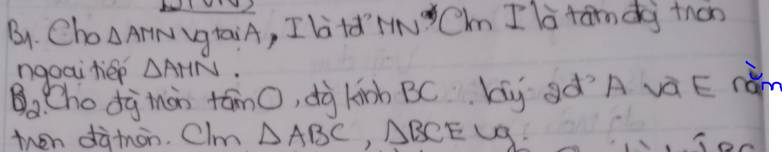
a: ΔAMN vuông tại A

mà AI là đường trung tuyến 

nên AI=IM=IN=MN/2

=>I là tâm đường tròn ngoại tiếp ΔAMN

b: Xét (O) có

ΔBAC nội tiếp

BC là đường kính

Do đó: ΔBAC vuông tại A

Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

Bài 3:

Nếu đáy lớn được tăng thêm 5 cm thì diện tích sẽ tăng một phần bằng 5 x chiều cao : 2

Vậy chiều cao của hình thang là:
$20\times 2:5=2$ (m) 

Diện tích hình thang ban đầu là:

$50\times 2:2=50$ (m²)

Không ai vẽ hình khi làm bài mặt cầu Oxyz đâu bạn, chỉ cần đại số hóa nó là được.

Gọi I là tâm mặt cầu, do mặt cầu tiếp xúc (Q) tại H nên \(IH\perp\left(Q\right)\)

\(\Rightarrow\) Đường thẳng IH nhận vtpt của (Q) là 1 vtcp

\(\Rightarrow\) IH nhận (1;1;-1) là 1 vtcp

Phương trình IH: \(\left\{{}\begin{matrix}x=1+t\\y=-1+t\\z=-t\end{matrix}\right.\)

I vừa thuộc IH vừa thuộc (P) nên là giao điểm của IH và (P)

\(\Rightarrow\) Tọa độ I thỏa mãn:

\(2\left(1+t\right)+\left(-1+t\right)+\left(-t\right)-3=0\)

\(\Rightarrow t=1\Rightarrow I\left(2;0;-1\right)\)

\(\Rightarrow\overrightarrow{IH}=\left(-1;-1;1\right)\Rightarrow R=IH=\sqrt{3}\)

Phương trình (S):

\(\left(x-2\right)^2+y^2+\left(z+1\right)^2=3\)

a: Xét (O) có

ΔAMB nội tiếp

AB là đường kính

Do đó: ΔAMB vuông tại M

=>\(\widehat{AMB}=90^0\)

b: Xét ΔOMC vuông tại M có MH là đường cao

nên \(HC\cdot HO=HM^2\left(1\right)\)

Xét ΔMAB vuông tại M có MH là đường cao

nên \(HA\cdot HB=HM^2\left(2\right)\)

Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)

c: Xét tứ giác AMBQ có

O là trung điểm của AB và MQ

Do đó: AMBQ là hình bình hành

Hình bình hành AMBQ có AB=MQ

nên AMBQ là hình bình hành

\(\dfrac{x+2}{x-3}< 0\)vì \(x+2>x-3\)

\(\left\{{}\begin{matrix}x+2>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x< 3\end{matrix}\right.\)<=> -2 < x < 3 

Bài 1: 

a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=6^2+8^2=100\)

hay BC=10(cm)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)

b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:

\(AF\cdot AB=AH^2\left(1\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:

\(AE\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

a: Sửa đề: A,B,M,O

Xét tứ giác BMOA có

\(\widehat{BMO}+\widehat{BAO}=90^0+90^0=180^0\)

=>BMOA là tứ giác nội tiếp

=>B,M,O,A cùng thuộc một đường tròn

b: Xét (O) có

BA,BM là tiếp tuyến

Do đó: BA=BM và OB là phân giác của \(\widehat{AOM}\)

=>\(\widehat{AOM}=2\cdot\widehat{AOB}\)

Xét (O) có

CA,CN là tiếp tuyến

Do đó: CA=CN và OC là phân giác của \(\widehat{AON}\)

=>\(\widehat{AON}=2\cdot\widehat{AOC}\)

\(\widehat{AON}+\widehat{AOM}=180^0\)(hai góc kề bù)

=>\(2\cdot\widehat{AOC}+2\cdot\widehat{AOB}=180^0\)

=>\(2\cdot\widehat{BOC}=180^0\)

=>\(\widehat{BOC}=90^0\)

Xét ΔOBC vuông tại O có OA là đường cao

nên \(OA^2=AB\cdot AC\)

mà AB=BM và AC=CN

nên \(OA^2=BM\cdot CN\)

c: BA=BM

=>B nằm trên đường trung trực của AM(1)

OA=OM

=>O nằm trên đường trung trực của AM(2)

Từ (1) và (2) suy ra BO là đường trung trực của AM

=>BO\(\perp\)AM tại trung điểm của AM

=>BO\(\perp\)AM tại H và H là trung điểm của AM

CA=CN

=>C nằm trên đường trung trực của AN(3)

OA=ON

=>O nằm trên đường trung trực của AN(4)

Từ (3) và (4) suy ra CO là đường trung trực của AN

=>CO\(\perp\)AN tại trung điểm của AN

=>CO\(\perp\)AN tại K và K là trung điểm của AN

Xét tứ giác AHOK có \(\widehat{AHO}=\widehat{AKO}=\widehat{HOK}=90^0\)

nên AHOK là hình chữ nhật