CHo parabol y= 1/2x^2 tìm trên (p) hai điểm A,B sao cho tam giác OAB đều

Những câu hỏi liên quan
cho parabol (P): y =x\(^2\) và đương thẳng (d): 2x + m + 1. Tìm m để (d) cắt (P) tại 2 điểm phân biệt A và B nằm về hai phía của trục tung sao cho diện tích tam giác OAB = 6
1. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(0;2), B(4;2). Tìm điểm M trên đoạn thẳng AB để parabol (P) đỉnh O và đi qua điểm M chia tam giác vuông OAB thành hai phần có diện tích bằng nhau.2. Cho hình phẳng (H ) giới hạn bởi các đường yx^2,y2x . Gọi S là tập hợp các giá trị của tham số thực k để đường thẳng x k2 chia hình phẳng (H) thành hai phần có diện tích bằng nhau. Hỏi tập hợp S có bao nhiêu phần tử?
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(0;2), B(4;2). Tìm điểm M trên đoạn thẳng AB để parabol (P) đỉnh O và đi qua điểm M chia tam giác vuông OAB thành hai phần có diện tích bằng nhau.
2. Cho hình phẳng (H ) giới hạn bởi các đường \(y=x^2,y=2x\) . Gọi S là tập hợp các giá trị của tham số thực k để đường thẳng x = k2 chia hình phẳng (H) thành hai phần có diện tích bằng nhau. Hỏi tập hợp S có bao nhiêu phần tử?
cho (P):y=X2
TÌM trên (p) 2 điểm A,B sao cho tam giác OAB đều
cho parabol(P): y=\(x^2\) và đường thẳng (d): y=2x+3
a) Vẽ đồ thị hai hàm số trên cùng một hê trục tọa độ
b') Tìm tọa độ giao điểm A và B của (P) và (d)
c) Tính diện tính tam giác OAB
Cho parabol (P): y = x 2 − 4x + 3 và đường thẳng d: y = mx + 3. Tìm tất cả các giá trị thực của mm để d cắt (P) tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng 9 2 .
A. m = 7.
B. m = −7.
C. m = −1,m = −7.
D. m = −1
Cho đường thẳng (d): y = x - 1 và parabol (P): y = x² + (2m + 1) - 3m² - 1 . Tim m để (d) cắt (P) tại hai điểm phân biệt A và B sao cho tam giác OAB có diện tích bằng 6
Trên mặt phẳng Oxy, cho hai điểm A(1; 3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB;
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
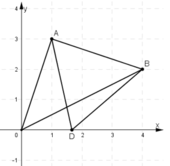
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
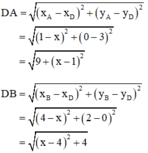
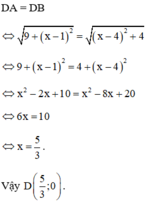
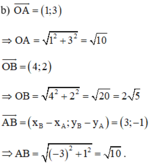
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
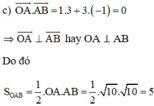
Đúng 0
Bình luận (0)
Cho parabol P() : y = 2x2 và đường thẳng (d) : y = x + 1
a) Vẽ (P) và (d) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm A và B của (P) và (d).
c) Tính diện tích tam giác OAB.
a: 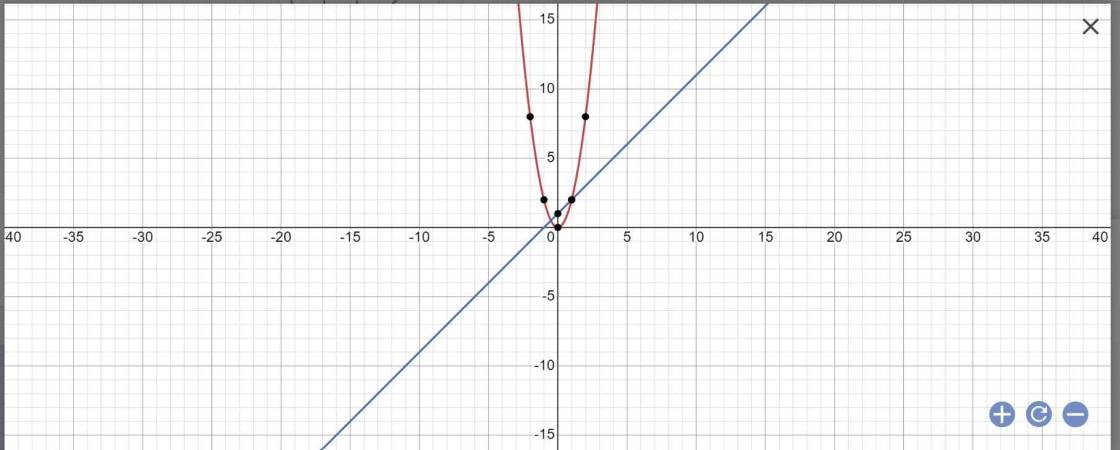
b: PTHĐGĐ là:
2x^2=x+1
=>2x^2-x-1=0
=>2x^2-2x+x-1=0
=>(X-1)(2x+1)=0
=>x=-1/2 hoặc x=1
=>y=2*1/4=1/2 hoặc y=2
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho Parabol (P):
y = x2 và đường thẳng (d): y = -x + 2
a) Tìm tọa độ giao điểm của (P) và (Q)
b) Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB.
\(\left\{{}\begin{matrix}\left(P\right):y=x^2\\\left(d\right):y=-x+2\end{matrix}\right.\)
a) Tọa độ giao điểm của (P) và (Q) là nghiệm của hệ phương trình
\(\left\{{}\begin{matrix}y=x^2\\y=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2+x-2=0\left(1\right)\end{matrix}\right.\)
\(pt\left(1\right)\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\) \(\left(a+b+c=1+1-2=0\right)\)
\(hpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\end{matrix}\right.\)
Vậy tọa độ giao điểm của (P) và (Q) là \(A\left(1;1\right)\&B\left(-2;4\right)\)
Đúng 1
Bình luận (0)
a) Phương trình hoành độ giao điểm :
x2 = - x + 2
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với x = 1 ta được y = 1
Với x = -2 ta được y = 4
Vậy tọa độ giao điểm là A(1; 1) ; B(-2;4)
b) Gọi C(-2 ; 0) ; D(1;0)
ta được \(S_{AOB}=S_{ABCD}-S_{BOC}-S_{AOD}\)
\(=\dfrac{\left(BC+AD\right).CD}{2}-\dfrac{BC.CO}{2}-\dfrac{AD.DO}{2}\)
\(=\dfrac{\left(4+1\right).3}{2}+\dfrac{4.2}{2}+\dfrac{1.1}{2}=12\) (đvdt)
Đúng 1
Bình luận (0)

















