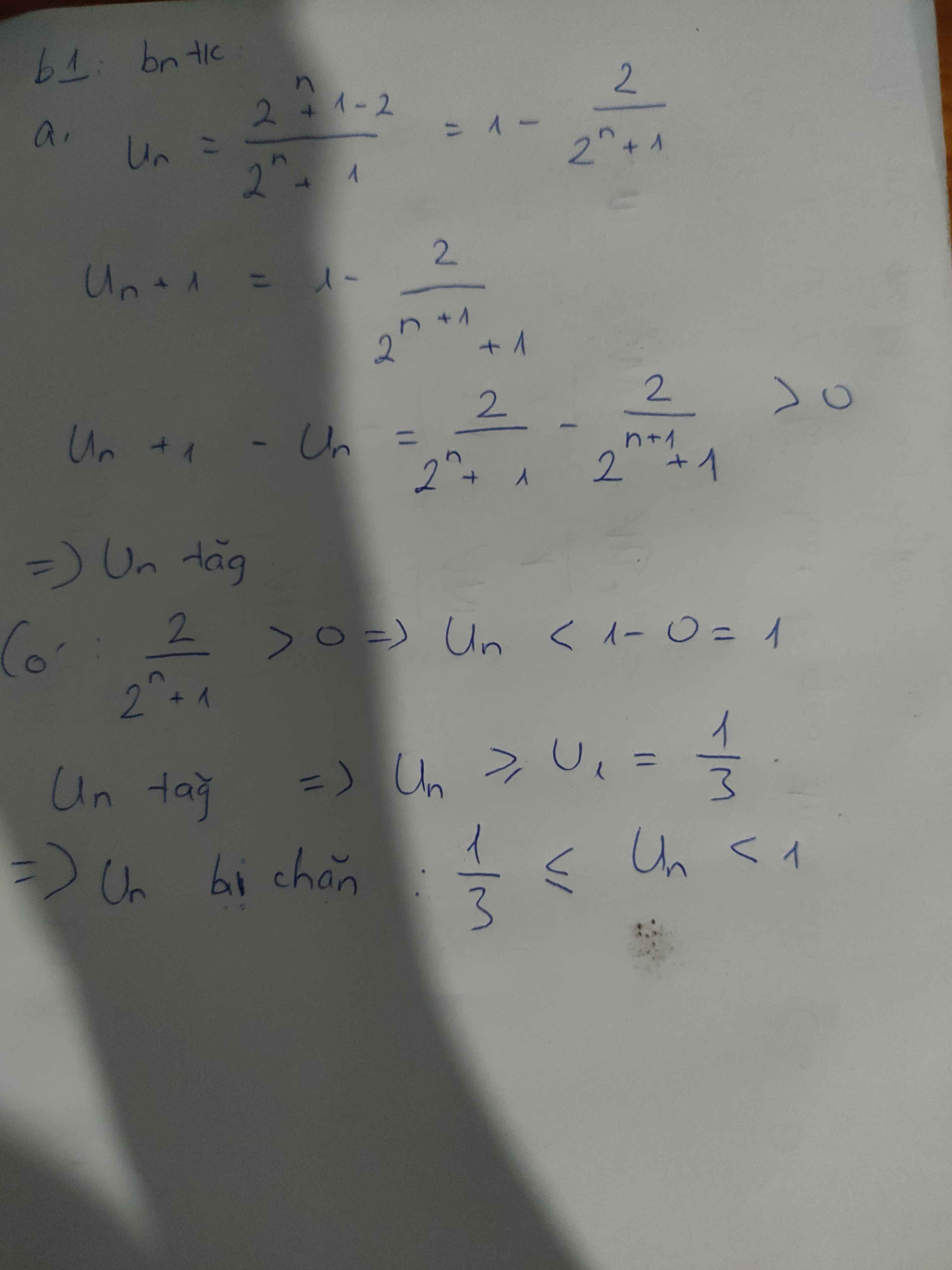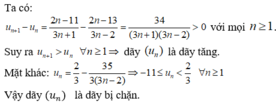xét tính bị chặn của dãy số (un) với un=\(\dfrac{n^2+1}{2n^2-3}\)

Những câu hỏi liên quan
Xét tính bị chặn của dãy số sau:
a) un=\(\dfrac{1}{2n^2-3}\)
b) un=\(\dfrac{1}{2n^2-1}\)
a: \(2n^2-3>=-3\)
\(\Leftrightarrow u_n=\dfrac{1}{2n^2-3}< =-\dfrac{1}{3}\)
=>Dãy số bị chặn trên ở -1/3
b: \(2n^2-1>=-1\)
=>\(u_n=\dfrac{1}{2n^2-1}< =\dfrac{1}{-1}=-1\)
=>Dãy số bị chặn trên ở -1
Đúng 0
Bình luận (0)
Bài 1: Xét tính tăng giảm của các dãy số (Un) với
a)\(Un=\dfrac{2^n-1}{2^n+1}\) b)\(Un=\left(-1\right)^n.n\)
Bài 2: Xét tính bị chặn của
\(Un=\sqrt[3]{n}-\sqrt[3]{n+1}\)
Cho dãy số (Un), với un = 1/1×2+ 1/2×3 + 1/3×4 +...+ 1/n(n+1). Xét tính tăng, giảm và bị chặn của dãy số.
\(u_n=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{n\left(n+1\right)}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(=1-\dfrac{1}{n+1}< 1\)
=>Hàm số bị chặn trên tại \(u_n=1\)
\(n+1>=1\)
=>\(\dfrac{1}{n+1}< =1\)
=>\(-\dfrac{1}{n+1}>=-1\)
=>\(1-\dfrac{1}{n+1}>=-1+1=0\)
=>Hàm số bị chặn dưới tại 0
\(u_n=1-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
\(\dfrac{u_n}{u_{n+1}}=\dfrac{n}{n+1}:\dfrac{n+1}{n+2}=\dfrac{n^2+2n}{n^2+2n+1}< 1\)
=>(un) là dãy số tăng
Đúng 1
Bình luận (0)
Xét tính tăng, giảm và bị chặn của dãy số
u
n
, biết:
u
n
2
n
-
13
3
n
-
2...
Đọc tiếp
Xét tính tăng, giảm và bị chặn của dãy số u n , biết: u n = 2 n - 13 3 n - 2
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
Xét tính tăng, giảm và bị chặn của dãy số
(
u
n
)
, biết:
u
n
2
n
−
13
3
n
−
2
A. Dãy số tăng, bị chặn B. Dãy số giảm, bị chặn C. Dãy số không tăng không giảm, không bị chặn D. Cả A, B, C đều sai
Đọc tiếp
Xét tính tăng, giảm và bị chặn của dãy số ( u n ) , biết: u n = 2 n − 13 3 n − 2
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
Ta có: u n = 2 ( n + 1 ) − 13 3 ( n + 1 ) − 2 = 2 n − 11 3 n + 1
Xét hiệu:
u n + 1 − u n = 2 n − 11 3 n + 1 − 2 n − 13 3 n − 2 = ( 2 n − 11 ) . ( 3 n − 2 ) − ( 2 n − 13 ) . ( 3 n + 1 ) ( 3 n + 1 ) ( 3 n − 2 ) = 6 n 2 − 4 n − 33 n + 22 − ( 6 n 2 + 2 n − 39 n − 13 ) ( 3 n + 1 ) . ( 3 n − 2 ) = 35 ( 3 n + 1 ) ( 3 n − 2 ) > 0
với mọi n ≥ 1 .
Suy ra u n + 1 > u n ∀ n ≥ 1 ⇒ dãy ( u n ) là dãy tăng.
Mặt khác: u n = 2 3 − 35 3 ( 3 n − 2 ) ⇒ u n < 2 3 ∀ n ≥ 1
Suy ra u n bị chặn trên
∀ n ≥ 1 : 3 n − 2 ≥ 1 ⇒ 35 3 ( 3 n − 2 ) ≤ 35 3.1 = 35 3 ⇒ u n ≥ 2 3 − 35 3 = − 11
Nên ( u n ) bị chặn dưới.
Vậy dãy ( u n ) là dãy bị chặn.
Chọn đáp án A.
Đúng 0
Bình luận (0)
Xét tính tăng, giảm và bị chặn của dãy số
(
u
n
)
, biết:
u
n
2
n
−
13
3
n
−
2
A. Dãy số tăng, bị chặn B. Dãy số giảm, bị chặn C. Dãy số không tăng không giảm, không bị chặn D. Cả A, B, C đều sai
Đọc tiếp
Xét tính tăng, giảm và bị chặn của dãy số ( u n ) , biết: u n = 2 n − 13 3 n − 2
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
Ta có: u n + 1 − u n = 2 n − 11 3 n + 1 − 2 n − 13 3 n − 2 = 35 ( 3 n + 1 ) ( 3 n − 2 ) > 0 với mọi n ≥ 1
Suy ra u n + 1 > u n ∀ n ≥ 1 ⇒ dãy ( u n ) là dãy tăng.
Mặt khác: u n = 2 3 − 35 3 ( 3 n − 2 ) ⇒ − 11 ≤ u n < 2 3 ∀ n ≥ 1
Vậy dãy ( u n ) là dãy bị chặn.
Chọn đáp án A
Đúng 0
Bình luận (0)
Chứng minh rằng: dãy số (Un) với \(U_n=\dfrac{n^2+1}{2n^2-3}\) là một dãy số bị chặn
\(u_n=\dfrac{n^2+1}{2n^2-3}\)
\(=\dfrac{1}{2}\cdot\dfrac{n^2+1}{n^2-1,5}\)
\(=\dfrac{1}{2}\left(\dfrac{n^2-1,5+2,5}{n^2-1,5}\right)=\dfrac{1}{2}\left(1+\dfrac{2.5}{n^2-1,5}\right)< \dfrac{1}{2}\)
=>(Un) là dãy số bị chặn
Đúng 1
Bình luận (0)
Xét tính tăng giảm và bị chặn của dãy số sau: (un): un = n3 + 2n + 1
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn C.
Ta có: un+1 – un = (n + 1)3 + 2(n + 1) – n3 – 2n = 3n2 + 3n + 3
Mặt khác: un > 1 và khi n càng lớn thì un càng lớn.
Vậy dãy (un) là dãy tăng và bị chặn dưới.
Đúng 0
Bình luận (0)
Xét tính tăng hay giảm và bị chặn của dãy số :
u
n
2
n
−
1
n
+
3
;
n
∈
N
*
A. Dãy số giảm, bị chặn trên B. Dãy số tăng, bị chặn dưới C. Dãy số tăng, bị chặn. D. Dãy số giảm, bị chặn dưới.
Đọc tiếp
Xét tính tăng hay giảm và bị chặn của dãy số : u n = 2 n − 1 n + 3 ; n ∈ N *
A. Dãy số giảm, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số tăng, bị chặn.
D. Dãy số giảm, bị chặn dưới.
Xét hiệu: u n + 1 − u n = 2 n + 1 n + 4 − 2 n − 1 n + 3
= 2 n 2 + 7 n + 3 − 2 n 2 − 7 n + 4 n + 4 n + 3 = 7 n + 4 n + 3 > 0 ; ∀ n ∈ N *
Vậy: ( u n ) là dãy số tăng.
Ta có u n = 2 n − 1 n + 3 = 2 ( n + 3 ) − 7 n + 3 = 2 − 7 n + 3
Suy ra: ∀ n ∈ ℕ * , u n < 2 nên ( u n ) bị chặn trên.
Vì ( u n ) là dãy số tăng ∀ n ∈ ℕ * , u 1 = 1 4 ≤ u n nên ( u n ) bị chặn dưới. Vậy ( u n ) bị chặn.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Xét tính tăng, giảm, bị chặn của dãy số (un) với un = 1/n+1
\(u_n=\dfrac{1}{n+1}\Rightarrow u_{n+1}=\dfrac{1}{n+2}\)
\(\Rightarrow u_n-u_{n+1}=\dfrac{1}{n+1}-\dfrac{1}{n+2}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}>0\)
\(\Rightarrow u_{n+1}< u_n\Rightarrow\) dãy giảm
Do \(\dfrac{1}{n+1}>0\Rightarrow\) dãy bị chặn dưới bởi 0
\(u_n-1=\dfrac{1}{n+1}-1=-\dfrac{n}{n+1}< 0\Rightarrow u_n< 1\)
\(\Rightarrow\) Dãy bị chặn trên bởi 1
\(\Rightarrow\) Dãy bị chặn
Đúng 1
Bình luận (0)