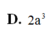Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm nằm trên các cạnh AC và AD; gọi O là điểm bên trong của tam giác BCD
Tìm giao điểm của AO và (AMN)
Cho tứ diện ABCD và ba điểm M, N,P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là:
A. Một tam giác
B. Một ngũ giác
C. Một đoạn thẳng
D. Một tứ giác
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng M N P là
A. Một tam giác
B. Một ngũ giá
C. Một đoạn thẳng
D. Một tứ giác
Đáp án A
Hiển nhiên thiết diện của hình tứ diện A B C D khi cắt bởi mặt phẳng M N P là một tam giác
Cho tứ diện ABCD và ba điểm M, N, P lần lượt nằm trên các cạnh AB, AC, AD mà không trùng với các đỉnh của tứ diện. Thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là
A. Một tam giác
B. Một ngũ giá
C. Một đoạn thẳng
D. Một tứ giác
Đáp án A
Hiển nhiên thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNP) là một tam giác.
Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm các cạnh AB và AC. E là điểm trên cạnh CD với ED=3EC. Thiết diện tạo bởi mp(MNE) và tứ diện ABCD là:
A. Tam giác MNE
B. Tứ giác MNEH với H là điểm bất kì trên cạnh BD
C. Hình bình hành MNEH với H là điểm trên cạnh BD mà EH//BC
D. Hình thang MNEH với H là điểm trên cạnh BD mà EH//BC
Đáp án C
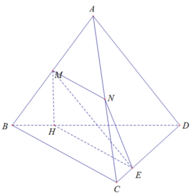
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang
Cho tứ diện ABCD. Qua điểm M nằm trên AC ta dựng một mặt phẳng (α) song song với AB và CD. Mặt phẳng này lần lượt cắt các cạnh BC, BD và AD tại N, P và Q.
a) Tứ giác MNPQ là hình gì?
b) Gọi O là giao điểm hai đường chéo của tứ giác MNPQ. Tìm tập hợp các điểm O khi M di động trên đoạn AC.
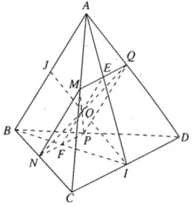
a) 
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và 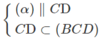
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và 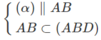 nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
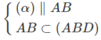 nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
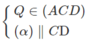
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.
Trong mp (ACD), kéo dài IJ cắt CD tại E thì E là giao điểm của CD và (IJK)
Cho tứ diện ABCD. Gọi M,K lần lượt là trung điểm của BC và AC. N là điểm trên cạnh BD sao cho BN=2ND. Gọi F là giao điểm của AD và mp(MNK). Trong các mệnh đề sau, mệnh đề nào đúng?
A. AF=3FD
B. AF=2FD
C. AF=FD
D. FD=2AF
Đáp án B
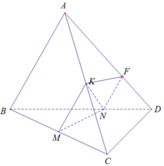
Xét (MNK) và (ABD) có:
N là điểm chung
AB // MK ⇒ A B ⫽ M N K
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua N và song song AB
d cắt AB tại điểm F cần tìm
Vì FN // AB ( cách dựng)
![]()
Cho tứ diện đều ABCD có cạnh bằng 3. Gọi M, N lần lượt là trung điểm các cạnh AD, BD. Gọi P là điểm trên cạnh AB sao cho 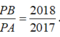 . Tính thể tích V của khối tứ diện PMNC
. Tính thể tích V của khối tứ diện PMNC
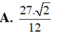

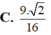

Cho tứ diện ABCD. Trên các cạnh AD và BC lần lượt lấy M, N sao cho AM = 3MD; BN = 3NC. Gọi P, Q lần lượt là trung điểm của AD và BC. Chứng minh các vectơ M N → , D C → , P Q → đồng phẳng.
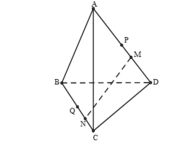
+) Do AM = 3MD; BN = 3NC suy ra:
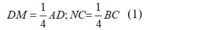
+) Do P và Q lần lượt là trung điểm của AD và BC nên :
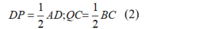
- Từ (1) và (2) suy ra: 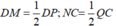
- Suy ra: M là trung điểm của DP; N là trung điểm CQ.
+) Ta có:

Cho tứ diện ABCD có các cạnh AB,AC, AD vuông góc với nhau từng đôi một và AB=3a, AC=6a, AD=4a. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CD, BD. Tính thể tích khối đa diện AMNP.
![]()
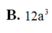
![]()