Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:
a) y = 4x3 + 3x2 – 36x + 6; b) \(y=\dfrac{x^2-2x-7}{x-4}\).
Xét tính đơn điệu và tìm cực trị của hàm số
y=-x4-2x2+3
\(y'=-4x^3-4x=-4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
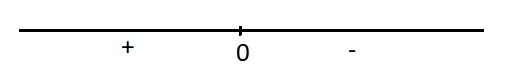
Hàm đồng biến trên \(\left(-\infty;0\right)\) và nghịch biến trên \(\left(0;+\infty\right)\)
Qua \(x=0\) ta thấy y' đổi dấu từ dương sang âm nên \(x=0\) là điểm cực đại
Xét các khoảng đơn điệu và tìm cực trị của hàm số
y = x + \(\sqrt{8-x^2}\)
Tập xác định: D=\(\left[-2\sqrt{2};2\sqrt{2}\right]\).
\(y'=1-\dfrac{x}{\sqrt{8-x^2}}\) = 0 \(\Rightarrow\) x=2.
Bảng biến thiên:
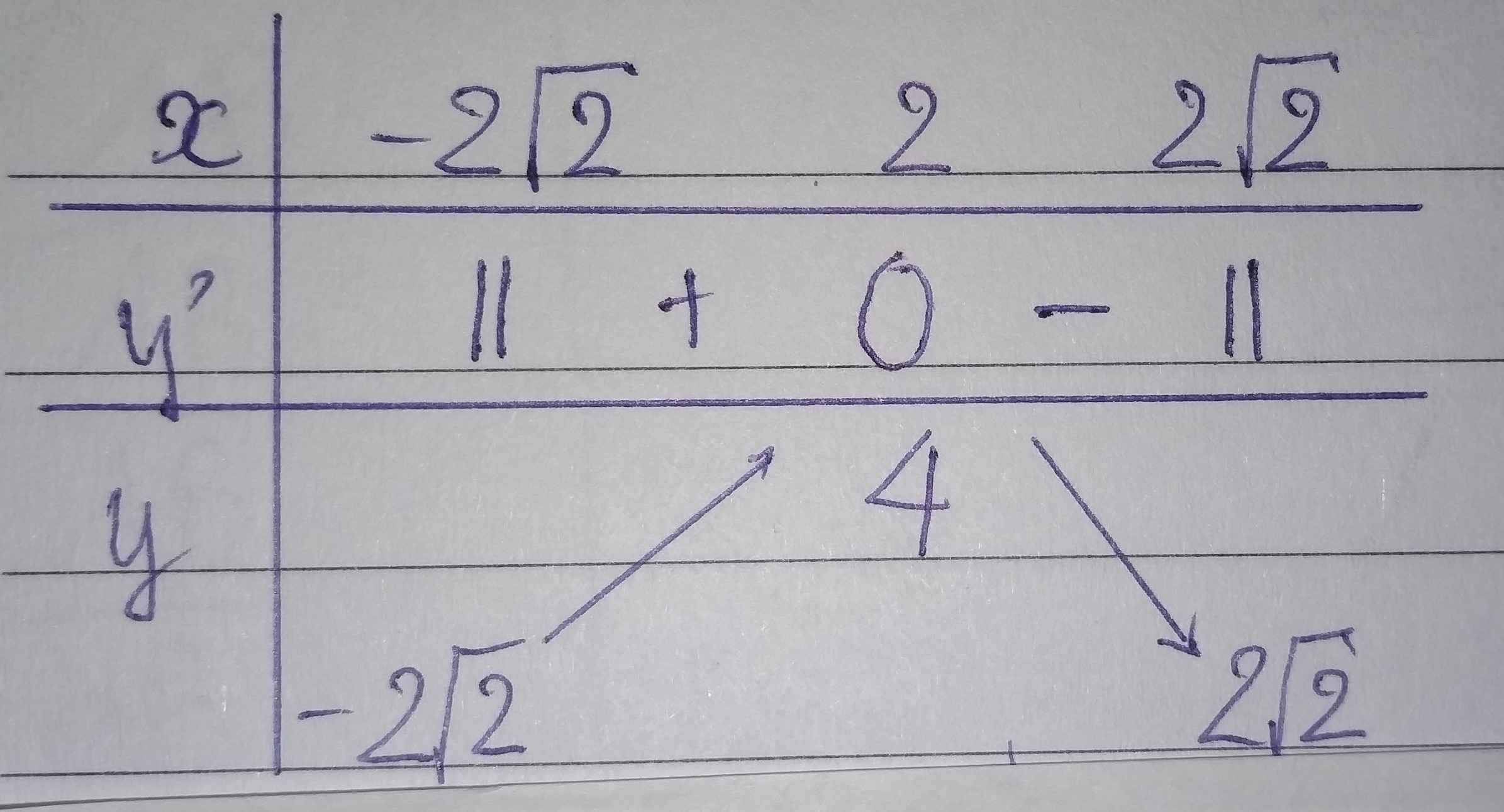
Vậy hàm số đã cho đồng biến trên khoảng (\(-2\sqrt{2}\);2), nghịch biến trên khoảng (2;\(2\sqrt{2}\)) và yCĐ=4 (tại x=2).
Tham khảo: Đồ thị:
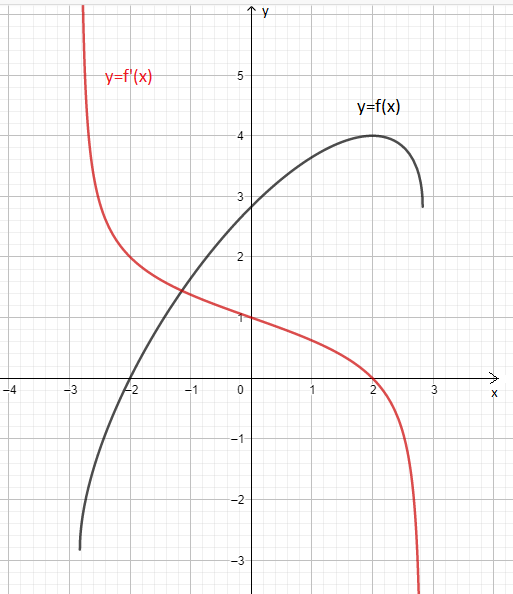
Xét tính đơn điệu và tìm cực trị của hàm số:
a) y=x+\(\sqrt{9-x^2}\)
b) y=\(\dfrac{-x^2-x-2}{x+2}\)
a. ĐKXĐ: \(-3\le x\le3\)
\(y'=1-\dfrac{x}{\sqrt{9-x^2}}=\dfrac{\sqrt{9-x^2}-x}{\sqrt{9-x^2}}=0\Rightarrow x=\dfrac{3\sqrt{2}}{2}\)
Dấu của y':
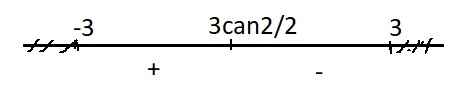
Hàm đồng biến trên \(\left(-3;\dfrac{3\sqrt{2}}{2}\right)\) và nghịch biến trên \(\left(\dfrac{3\sqrt{2}}{2};3\right)\)
b.
ĐKXĐ: \(x\ne2\)
\(y'=\dfrac{\left(-2x-1\right)\left(x+2\right)+x^2+x+2}{\left(x+2\right)^2}=\dfrac{-x^2-4x}{\left(x+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
Dấu của y':
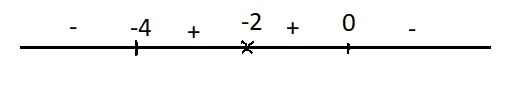
Hàm đồng biến trên các khoảng \(\left(-4;-2\right)\) và \(\left(-2;0\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-4\right)\) và \(\left(0;+\infty\right)\)
Xét tính đơn điệu của hàm số: f(x) = x + |3x2 + 9x -12|
Xét tính đơn điệu của các hàm số sau: y = x 3 x 2 - 6
TXĐ: (- ∞ ; 6 ) ∪ ( 6 ; + ∞ )
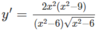
y’ = 0 ⇔ x = 3 hoặc x = -3
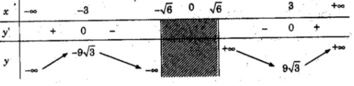
Vậy hàm số đồng biến trên các khoảng (- ∞ ; -3), (3; + ∞ ), nghịch biến trên các khoảng (-3; − 6 − 6 ), ( 6 ; 3).
Xét tính đơn điệu và vẽ đồ thị hàm số sau:
A)y=2x+1
B)y=-x+1
C)y=\(\dfrac{1-x}{2}\)
D)y=\(\dfrac{-x}{4}\)+2
a: Hàm số đồng biến trên R
b: Hàm số nghịch biến trên R
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 3 x 2 + 3 m 2 - 1 x - 3 m 2 - 1 có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ O.
A. m = ± 1 2
B. m = 1 2
C. m = -1
D. m = ± 1
Chọn A
![]()
![]()
![]() là tam thức bậc hai có ∆' = m2.
là tam thức bậc hai có ∆' = m2.
Do đó: y có cực đại cực tiểu ⇔ y’ có hai nghiệm phân biệt
⇔ g(x) có hai nghiệm phân biệt ⇔ ∆' > 0 ⇔ m ≠ 0. (1)
Khi đó, y’ có các nghiệm là: 1 ± m
→ tọa độ các điểm cực trị của đồ thị hàm số là
![]()
![]()
![]()
![]()
![]()
Để A và B cách đều gốc tọa độ khi và chỉ khi :
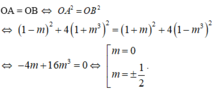
Đối chiếu với điều kiện (1), ta thấy chỉ m = ± 1 2 thỏa mãn yêu cầu bài toán.
Cho hàm số y = f ( x ) có đồ thị như hình vẽ.
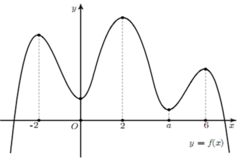
Biết tất cả các điểm cực trị của hàm số y = f ( x ) là – 2, 0, 2, a , 6 với 4 < a < 6. Số điểm cực trị của hàm số y = f ( x 6 − 3 x 2 ) là
A. 8
B. 11
C. 9
D. 7
Gọi x1; x2 là hai điểm cực trị của hàm số y= 4x3+mx2-3x. Tìm các giá trị thực của tham số m để x1+4x2=0
A. m = ± 9 2
B. m=±1
C. m=0
D. m= ±2
Ta có y’=12x2+2mx-3.
Do ∆ ' = m 2 + 36 > 0 , ∀ m ∈ ℝ nên hàm số luôn có hai điểm cực trị x1; x2.
Theo Viet, ta có x 1 + x 2 = - m 6 x 1 x 2 = - 1 4
Mà x1+4x2=0 suy ra
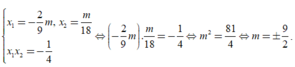
Chọn A.
Cho hàm số y = x 3 - 3 x 2 + m x - 1 với m là tham số thực. Tìm tất cả các giá trị của tham số m để hàm số đạt cực trị tại hai điểm x 1 , x 2 thỏa x 1 2 + x 2 2 = 6 .
A. 3.
B. -1.
C. 1.
D. -3.