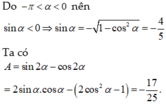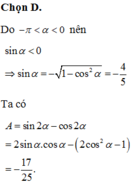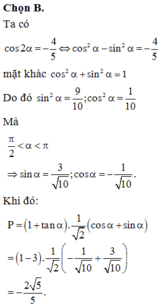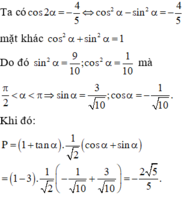Cho α là góc nhọn tính giá trị của biểu thức: A = sin6α + 3sin2α.cos2α + cos2α

Những câu hỏi liên quan
Cho
α
là góc nhọn bất kỳ. Khi đó
C
sin
6
α
+
cos
6
α
+
3
sin
2
α
.
cos
2
α
bằng: A. C
1
-
3
sin
2
α
.
cos
2...
Đọc tiếp
Cho α là góc nhọn bất kỳ. Khi đó C = sin 6 α + cos 6 α + 3 sin 2 α . cos 2 α bằng:
A. C = 1 - 3 sin 2 α . cos 2 α
B. C = 1
C. C = sin 2 α . cos 2 α
D. C = 3 sin 2 α . cos 2 α - 1
Ta có:

= sin 6 α + cos 6 α + 3 sin 2 α . cos 2 α . ( sin 2 α + cos 2 α ) v ì sin 2 α + cos 2 α = 1
= ( sin 2 α ) 3 + 3 sin 2 α 2 cos 2 + 3 sin 2 α . cos 2 α 2 + cos 2 α 3

Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Chứng minh rằng:
a) sin4 α+ sin2α.cos2α+cos2α=1
b)(1+tanα).(1+cotα).sinα.cosα=1+2.sinα.cosα
c)sin6α+cos6α+3sin2α.cos2α=1
a: \(=\left(\sin^2\alpha+\cos^2\alpha\right)^2=1^2=1\)
Đúng 0
Bình luận (0)
Cho góc
α
thỏa mãn
cos
α
3
5
và
-
π
α
0
A
sin
2
α
-
cos
2
α
. Tính giá trị biểu thức .
A
sin
2
α
-
cos
2
α
A.
-
26
25
B.
-
13
25
C. ...
Đọc tiếp
Cho góc α thỏa mãn cos α = 3 5 và - π < α < 0 A = sin 2 α - cos 2 α . Tính giá trị biểu thức . A = sin 2 α - cos 2 α
A. - 26 25
B. - 13 25
C. 3 25
D. - 17 25
Cho góc
α
thỏa mãn:
cos
α
3
5
v
à
-
π
α
0
.Tính giá trị biểu thức:
A
sin
2
α
-
cos
2
α
A.
-
26
25
B....
Đọc tiếp
Cho góc α thỏa mãn: cos α = 3 5 v à - π < α < 0 .Tính giá trị biểu thức: A = sin 2 α - cos 2 α
A. - 26 25
B. - 13 25
C. 3 25
D. - 17 25
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trịcủa các góc nhọn α.a) A cos4α + 2cos2α . sin2α + sin4ab) B sin4α + cos2α . sin2α + cos2αc) C 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos αd) D (tan α - cot α )2 - (tan α + cot α )2e) E 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)f) F dfrac{1}{1+sintext{α}}+dfrac{1}{1-sintext{α}}-2 tan2α
Đọc tiếp
Chứng minh giá trị các biểu thức sau không phụ thuộc vào giá trị
của các góc nhọn α.
a) A = cos4α + 2cos2α . sin2α + sin4a
b) B = sin4α + cos2α . sin2α + cos2α
c) C = 2(sin α - cos α )2 - (sin α + cos α )2 + 6sin α . cos α
d) D = (tan α - cot α )2 - (tan α + cot α )2
e) E = 4 cos2 α + (sin α - cos α)2 + (sin α+ cosα)2 + 2(sin2 α -cos2 α)
f) F = \(\dfrac{1}{1+sin\text{α}}\)+\(\dfrac{1}{1-sin\text{α}}\)-2 tan2α
Cho
cos
2
α
-
4
5
với
π
2
α
π
Tính giá trị của biểu thức:
P
1
+
tan
α
cos
π
4
-
α
.Đáp án...
Đọc tiếp
Cho cos 2 α = - 4 5 với π 2 < α < π Tính giá trị của biểu thức: P = 1 + tan α cos π 4 - α .Đáp án đúng của P là:
A.P= - 2 5 3
B.P= - 2 5 5
C.P= - 5 5
D.P= - 2 3 5
Cho
α
là góc nhọn bất kỳ. Biểu thức
Q
cos
2
α
−
sin
2
α
c
o
s
α
.
sin
α
bằng: A. Q cot
α
− tan
α...
Đọc tiếp
Cho α là góc nhọn bất kỳ. Biểu thức Q = cos 2 α − sin 2 α c o s α . sin α bằng:
A. Q = cot α − tan α
B. Q = cot α + tan α
C. Q = tan α − cot α
D. Q = 2 tan α
Với tan α = sin α cos α ; cot α = cos α sin α ta có:
Q = Q = cos 2 α − sin 2 α c o s α . sin α = cos 2 α sin α . cos α − sin 2 α sin α . cos α = cos α sin α − sin α cos α
= cot α − tan α
Vậy Q = cot α − tan α
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho
cos
2
α
-
4
5
với
π
2
α
π
. Tính giá trị của biểu thức:
P
1
+
tan...
Đọc tiếp
Cho cos 2 α = - 4 5 với π 2 < α < π . Tính giá trị của biểu thức: P = 1 + tan α cos π 4 - α .Đáp án đúng của P là:
A. P = - 2 5 3
B. P = - 2 5 5
C. P = - 5 5
D. P = - 2 3 5
cho cosα=\(\dfrac{3}{5}\)(0<α<\(\dfrac{\pi}{2}\))
a. Tính sinα.
b. Tính giá trị biểu thức P=cos2α-cosα.
Cho góc nhọn α. Giá trị của biểu thức
P
s
i
n
2
90
°
−
α
+
s
i
n
2
α
là A.1 B. 2 C.
2
s
i
n
2
90
°
−
α
D.
2
s
i
n...
Đọc tiếp
Cho góc nhọn α. Giá trị của biểu thức P = s i n 2 90 ° − α + s i n 2 α là
A.1
B. 2
C. 2 s i n 2 90 ° − α
D. 2 s i n 2 α
Đáp án A
P = s i n 2 90 ° − α + s i n 2 α = c o s 2 α + s i n 2 α = 1
Đúng 0
Bình luận (0)