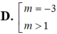giải phương trình nghiệm nguyên: x4 - 2y4 - x2y2 - 4x2 - 7y2 -5 =0
Những câu hỏi liên quan
Cho hàm số
f
x
x
4
-
4
x
2
+
3
có đồ thị là đường cong trong hình bên. Hỏi phương trình
x
4
-
4
x
2
+
3
4...
Đọc tiếp
Cho hàm số f x = x 4 - 4 x 2 + 3 có đồ thị là đường cong trong hình bên. Hỏi phương trình x 4 - 4 x 2 + 3 4 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có bao nhiêu nghiệm thực phân biệt
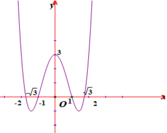
A. 8
B. 10
C. 8
D. 4
Cho phương trình x 4 - 4 x 2 - 5 - m = 0 có 6 nghiệm phân biệt thỏa mãn a < m < b thì a + b là:
A. -14
B. 9
C. 14
D. 5
Đáp án C.
Xét hàm số x 4 - 4 x 2 + 5 ⇒ y ' = 0
⇔ 4 x 3 - 8 x = 0 ⇔ x = 0 x = ± 2
Bảng biến thiên:
⇒ Đồ thị hàm số y = x 4 - 4 x 2 - 5 ( C )
Từ (C) giữ phần đồ thị phía trên, bỏ phía dưới sau khi lấy đối xứng qua Ox
⇒ Đồ thị hàm số y = x 4 - 4 x 2 - 5 (hình vẽ)
⇒ Phương trình y = x 4 - 4 x 2 - 5 = m có 6 nghiệm ⇔ 5 < m < 9 ⇒ a + b = 14 .
Đúng 0
Bình luận (0)
Cho phương trình x 4 − 4 x 2 − 5 − m = 0 có 6 nghiệm phân biệt thỏa mãn a<m<b thì a+b là
A. -14
B. 9
C. 14
D. 5
Cho hàm số
y
f
x
x
4
-
4
x
2
+
3
có đồ thị là đường cong trong hình vẽ bên. Hỏi phương trình
x...
Đọc tiếp
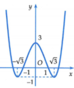
Cho hàm số y = f x = x 4 - 4 x 2 + 3 có đồ thị là đường cong trong hình vẽ bên. Hỏi phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có bao nhiêu nghiệm thực phân biệt?
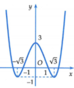
A. 9.
B. 10.
C.8.
D. 4
Chọn đáp án B
Ta có
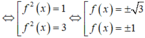
Quan sát đồ thị của hàm số y = f(x) ta thấy:
Phương trình f x = - 3 không có nghiệm; phương trình f x = - 1 có 2 nghiệm;
phương trình f x = 1 có 4 nghiệm; phương trình f x = 3 có 4 nghiệm.
Vậy phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có 10 nghiệm.
Đúng 0
Bình luận (0)
Tìm m để bất phương trình:
x
4
−
4
x
2
−
m
+
1
≤
0
có nghiệm thực A.
m
≥
−
3
B.
m
≤
1
C.
m
≥
1
D.
m
≤
−
3
Đọc tiếp
Tìm m để bất phương trình: x 4 − 4 x 2 − m + 1 ≤ 0 có nghiệm thực
A. m ≥ − 3
B. m ≤ 1
C. m ≥ 1
D. m ≤ − 3
Đáp án A
Bất phương trình ⇔ x 4 − 4 x 2 + 4 ≤ x 2 − 2 2 ≤ m + 3
Để bất phương trình có nghiệm thực thì m + 3 ≥ min x 2 − 2 2 = 0 ⇔ m ≥ − 3
Đúng 0
Bình luận (0)
Số nghiệm của hệ phương trình
x
4
-
4
x
2
+
y
2
-
6
y
+
9...
Đọc tiếp
Số nghiệm của hệ phương trình x 4 - 4 x 2 + y 2 - 6 y + 9 = 0 x 2 y + x 2 + 2 y - 22 = 0 là:
A. 4
B. 1
C. 2
D. 3
Giải các phương trình sau:a)
x
+
2
3
+
x
+
1
3
0
;
b)
2
x
4
+
3
x
2
−
5
0
;
c)
x...
Đọc tiếp
Giải các phương trình sau:
a) x + 2 3 + x + 1 3 = 0 ;
b) 2 x 4 + 3 x 2 − 5 = 0 ;
c) x 4 − 8 x 3 − 9 x 2 = 0 ;
d) x 3 − 4 x 2 + 4 − x = 0 .
Cho hàm số
y
x
4
−
4
x
2
+
2
có bảng biến thiên như hình vẽ dưới đây. Tìm m để phương trình
x
4
−
4
x
2
+
2
m
có đúng 5 nghiệm phân biệt. A....
Đọc tiếp
Cho hàm số y = x 4 − 4 x 2 + 2 có bảng biến thiên như hình vẽ dưới đây. Tìm m để phương trình x 4 − 4 x 2 + 2 = m có đúng 5 nghiệm phân biệt.
A. m > 2
B. 0 < m < 2
C. m = 0
D. m = 2
Không giải phương trình, hãy tính tổng và tích các nghiệm (nếu có) của mỗi phương trình sau:
4x2 + 2x – 5 = 0
Phương trình 4x2 + 2x – 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x1; x2
Theo hệ thức Vi-et ta có: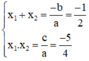 
Đúng 0
Bình luận (0)
Tìm m để phương trình
x
4
-
4
x
2
+
1
m
có đúng hai nghiệm
Đọc tiếp
Tìm m để phương trình x 4 - 4 x 2 + 1 = m có đúng hai nghiệm
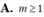
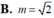
