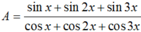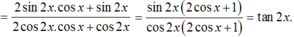Bạn kiểm tra lại đề bài câu 1, câu này chỉ có thể rút gọn đến \(2cot^2x+2cotx+1\) nên biểu thức ko hợp lý

Đồng thời kiểm tra luôn đề câu 2, trong cả 2 căn thức đều xuất hiện \(6sin^2x\) rất không hợp lý, chắc chắn phải có 1 cái là \(6cos^2x\)

Câu 1 đề vẫn có vấn đề:

\(=\dfrac{1+cotx}{1-cotx}-\dfrac{2\left(1+cot^2x\right)cot^2x}{\left(tanx-1\right)\left(tan^2x+1\right)cot^2x}=\dfrac{1+cotx}{1-cotx}-\dfrac{2cot^2x}{tanx-1}\)

\(=\dfrac{1+cotx}{1-cotx}-\dfrac{2cot^3x}{1-cotx}=\dfrac{1+cotx-2cot^3x}{1-cotx}\)

\(=\dfrac{\left(1-cotx\right)\left(1+2cotx+2cot^2x\right)}{1-cotx}=1+2cotx+2cot^2x\)

Có thể coi như ko thể rút gọn tiếp

2.

\(\sqrt{\left(1-cos^2x\right)^2+6cos^2x+3cos^4x}+\sqrt{\left(1-sin^2x\right)^2+6sin^2x+3sin^4x}\)

\(=\sqrt{4cos^4x+4cos^2x+1}+\sqrt{4sin^4x+4sin^2x+1}\)

\(=\sqrt{\left(2cos^2x+1\right)^2}+\sqrt{\left(2sin^2x+1\right)^2}\)

\(=2\left(cos^2x+sin^2x\right)+2=4\)

\(B=\dfrac{1-4\sin^2x\cdot\cos^2x}{\sin^2x+2\sin x\cdot\cos x+\cos^2}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}+2\sin x\cdot\cos x\\ B=\dfrac{1-4\sin^2x\cdot\cos^2x+4\sin^2x\cdot\cos^2x}{2\sin x\cdot\cos x}=\dfrac{1}{2\sin x\cdot\cos x}\)

\(sinx+cosx=m\Leftrightarrow\left(sinx+cosx\right)^2=m^2\)

\(\Leftrightarrow1+2sinx.cosx=m^2\Rightarrow sinx.cosx=\dfrac{m^2-1}{2}\)

\(A=sin^2x+cos^2x=1\)

\(B=sin^3x+cos^3x=\left(sinx+cosx\right)^3-3sinx.cosx\left(sinx+cosx\right)\)

\(=m^3-\dfrac{3m\left(m^2-1\right)}{2}=\dfrac{2m^3-3m^3+3m}{2}=\dfrac{3m-m^3}{2}\)

\(C=\left(sin^2+cos^2x\right)^2-2\left(sinx.cosx\right)^2=1-2\left(\dfrac{m^2-1}{2}\right)^2\)

\(D=\left(sin^2x\right)^3+\left(cos^2x\right)^3=\left(sin^2x+cos^2x\right)^3-3\left(sin^2x+cos^2x\right)\left(sinx.cosx\right)^2\)

\(=1-3\left(\dfrac{m^2-1}{2}\right)^2\)

Chọn C.

Ta có:

\(\left(sin^4x+cos^4x+cos^2x.sin^2x\right)^2-sin^8x\)

\(=\left(sin^4x+cos^2x\left(cos^2x+sin^2x\right)\right)^2-sin^8x\)

\(=\left(sin^4x+cos^2x\right)^2-sin^8x=\left(sin^4x+cos^2x-sin^4x\right)\left(sin^4x+cos^2x+sin^4x\right)\)

\(=cos^2x\left(2sin^4x+cos^2x\right)=2sin^4x.cos^2x+cos^4x\)

Tương tự: \(\left(sin^4x+cos^4x+sin^2xcos^2x\right)^2-cos^8x\)

\(=\left(cos^4x+sin^2x\left(sin^2x+cos^2x\right)\right)^2-cos^8x\)

\(=\left(cos^4x+sin^2x\right)^2-cos^8x\)

\(=\left(cos^4x+sin^2x-cos^4x\right)\left(cos^4x+sin^2x+cos^4x\right)\)

\(=sin^2x\left(2cos^4x+sin^2x\right)=2sin^2x.cos^4x+sin^4x\)

\(\Rightarrow M=2sin^2x.cos^4x+2sin^2x.cos^2x+sin^2x+cos^4x\)

\(M=2sin^2x.cos^2x\left(cos^2x+sin^2x\right)+sin^4x+cos^4x\)

\(M=2sin^2x.cos^2x+sin^4x+cos^4x\)

\(M=\left(sin^2x+cos^2x\right)^2=1\)

\(A=\dfrac{sin^2x-cos^2x.\left(1-cos^2x\right)}{cos^2x-sin^2x.\left(1-sin^2x\right)}=\dfrac{sin^2x-cos^2x.sin^2x}{cos^2x-sin^2x.cos^2x}\\ =\dfrac{sin^2x.\left(1-cos^2x\right)}{cos^2x.\left(1-sin^2x\right)}=\dfrac{sin^2x.sin^2x}{cos^2x.cos^2x}=\dfrac{sin^4x}{cos^4x}.\)

\(A=\cos^4x+2\sin^2x.\cos^2x\left(\sin^2x+\cos^2x\right)+\sin^4x+1\)

\(=\cos^4x+2\sin^2x.\cos^2x+\sin^4x+1\)

\(=\left(\sin^2x+\cos^2x\right)^2+1=1+1=2\)

(sin 1 độ + sin 2 độ + ... + sin 89 độ) - (cos 1 độ + cos 2 độ + ... + cos 89 độ)

=(cos 89 độ +... + cos 2 độ +cos 1 độ) - (cos 1 độ + cos 2 độ + ... + cos 89 độ)

=0

\(A=\sqrt{\left(1-cos^2x\right)^2+4cos^2x}+\sqrt{\left(1-sin^2x\right)^2+4sin^2x}\)

\(=\sqrt{cos^4x+2cos^2x+1}+\sqrt{sin^4x+2sin^2x+1}\)

\(=\sqrt{\left(cos^2x+1\right)^2}+\sqrt{\left(sin^2x+1\right)^2}\)

\(=sin^2x+cos^2x+2=3\)

b/

\(3\left(sin^8x-cos^8x\right)=3\left(sin^4x+cos^4x\right)\left(sin^4x-cos^4x\right)\)

\(=3\left(sin^4x+cos^4x\right)\left(sin^2x-cos^2x\right)\)

\(=3sin^6x-3sin^4x.cos^2x+3sin^2x.cos^4x-3cos^6x\)

\(\Rightarrow B=-5sin^6x-3sin^4x.cos^2x+3sin^2x.cos^4x+cos^6x+6sin^4x\)

\(=-5sin^6x-3sin^4x\left(1-sin^2x\right)+3cos^4x\left(1-cos^2x\right)+cos^6x+6sin^4x\)

\(=-2sin^6x-2cos^6x+3sin^4x+3cos^4x\)

\(=-2\left(1-3sin^2x.cos^2x\right)+3\left(1-2sin^2x.cos^2x\right)\)

\(=-2+3=1\)