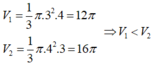cho ∆abc có ab

Những câu hỏi liên quan
1 Khi chia STN a cho 54 ta được số dư là 38 , khi chia cho 18 ta được thương là 14 và còn dư . Tim số a
2 . thay các chữ số thích
ab + bc + ca = abc ( ab , bc , ca , abc co gạch trên đầu )
abc + ab + a = 874( abc , ab có gạch trên đầu )
abc + ab + a = 1037 ( abc , ab có gạch trên đầu )
1) a chia cho 54 dư 38 => a = 54k + 38 = 18.3k + 36 + 2 = 18.(3k +2) + 2
=> a chia cho 18 dư 2; a chia hco 18 được thương là 14
=> a = 18.14 + 2 = 254
Đúng 0
Bình luận (0)
b) => 100a + 10b + c + 10a + b + a = 874
=> 111a + 11b + c = 874
=> 111a < 874 => a < 8
Hơn nữa, 11b + c < 11.10 + 10 = 120 => 111a + 11b + c < 120 + 111a
=> 111a + 120 > 874 => 111a > 754 => a > 6 mà a < 8 nên a = 7
vậy 777 + 11b + c = 874 => 11b + c = 874 - 777 = 97
Tương tự, => b < 9 và b > 7 => b = 8 => 88 + c = 97 => c = 9
Vậy abc = 789
Đúng 0
Bình luận (0)
c) => 100a + 10b + c + 10a + b + a = 1037
=> 111a + 11b + c = 1037
Nhận xét: 111a < 1037 => a < 10
Hơn nữa, 11b + c < 11.10 + 10 = 120 => 1037 < 120 + 111a => 111a > 1037 - 120 = 917 => a > 8 mà a < 10
nên a = 9
=> 999 + 11b + c = 1037
=> 11b + c = 38 => 11b < 38 => b < 4 hơn nữa c lớn nhất bằng 9 nên 11b nhỏ nhất là 38 - 9 = 28 tức là 11b > 28 => b > 2
vậy b = 3
=> c = 5
Vậy abc = 935
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc có ab = 15cm ac=20cm trên cạnh ab và ac lấy hai điểm DE sao cho cho ab=8 ae=6 hỏi tam giác abc, tam giác ade có đồng dạng không
Xét tam giác ABC và tam giác AED có
\(\hept{\begin{cases}A:gócchung\\\frac{AE}{AB}=\frac{AD}{AC}\left(\frac{8}{20}=\frac{6}{15}\right)\end{cases}}\)
Vậy tam giác ABC đồng dạng với tam giác AED (c-g-c)
Đúng 0
Bình luận (0)
easy :>
Ta có : \(\frac{AE}{AB}=\frac{6}{15}=\frac{2}{5} ;\frac{ AD}{AC}=\frac{8}{20}=\frac{2}{5}\)
\(\Rightarrow\frac{AE}{AB}=\frac{AB}{AC}\)
Xét 2 tam giác : ADE và ACB có :
\(\widehat{A}\)chung
\(\frac{AE}{AB}=\frac{AB}{AC}\)
\(\Rightarrow\Delta ADE~\Delta ACB\left(TH2\right)\)
1 ) Cho tam giác ABC có góc A nhọn , AB=4 , AC=5 và diện tích tam giác ABC =8 . Tính BC
2 ) Cho tam giác ABC có AB=3 , góc ACB = 45° , góc ABC = 60° . Tính BC
em mới học lớp 7 hà
năm nay lên lớp 8 =)))))
Đúng 0
Bình luận (0)
1)Ta có: \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
\(\Leftrightarrow8=\dfrac{1}{2}\times4\times5\times sinA\)
\(\Leftrightarrow\sin A=0,8\)
Lại có: \(\left(\sin A\right)^2+\left(\cos A\right)^2=1\Leftrightarrow\cos A=0,6.\)
Áp dụng định lí hàm số cosin:
\(BC^2=AB^2+AC^2-2AB\times AC\times\cos A\)
\(\Leftrightarrow BC^2=4^2+5^2-2\times4\times5\times0,6=17\)
\(\Leftrightarrow BC=\sqrt{17}.\)
2) Trong \(\Delta ABC\) có: \(g\text{ó}cA+g\text{óc}B+g\text{óc}C=180^o\)
=> BAC=75o.
Áp dụng định lí hàm số sin:
\(\dfrac{AB}{\sin C}=\dfrac{BC}{\sin A}\Leftrightarrow\dfrac{3}{\sin45^o}=\dfrac{BC}{\sin75^o}\)
\(\Leftrightarrow BC=\dfrac{3+3\sqrt{3}}{2}\).
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC= 1cm; AC= 7cm và độ dài cạnh AB là một số nguyên (cm).Tính độ dài AB và cho biết tam giác ABC là tam giác gì?
A. AB= 7cm và tam giác ABC vuông tại A
B. AB= 7cm và tam giác ABC cân tại A
C. AB= 7cm và tam giác ABC vuông cân tại A
D. AB= 8cm và tam giác ABC vuông tại B
Xem thêm câu trả lời
1. cho tam giác ABC có góc B = góc C. CMR AB=AC.
2. cho tam giác ABC có AB=AC. CMR góc B = góc C
minh vua tik ban do , ban tik lai minh di
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc ABC=75 độ; CH vuông góc AB;CH=AB/2. Chứng minh AB=AC
1 .Cho tam giác Abc vuông ở A . có chu vi = 24cm . có cạnh Ab = 3/4 Ac ; Bc =10cm . tính Sabc
2. Cho ∆ ABC có cạnh BC = 32cm . nếu kéo dài cạnh AB thêm 4cm thì Sabc sẽ tăng 52cm2 . tính SAbc
3. ∆ abc có ab = 50 cm . nếu kéo dài bc thêm 1 đoạn cd = 30cm thì ∆ abc là ∆ cân vs ab = ad và ∆ acd có chiều cao hạ từ c=18cm . tính S abc biết chu vi ABD là 180cm
Giải hộ ☺
Cho tam giác ABC có ABC =50 BAC=100trên cạnh AB lấy M sao cho AM=AC so sánh CM với AB
Cho △ABC có \(\widehat{A}\)=45 độ, \(\widehat{B}\)=75 độ thì:
a. BC<AB<AC
b. BC<AC<AB
c. AB<AC<BC
d. AC<BC<AB
Xem thêm câu trả lời
Cho
∆
A
B
C
vuông tại A, cạnh AB4,BC5. Quay
∆
A
B
C
quanh AB được khối nón có thể tích
V
1
, quay
∆
A
B
C
quanh AC được khối nón có thể tích
V
2
thì: A.
V
1
V
2
12
π
B.
V...
Đọc tiếp
Cho ∆ A B C vuông tại A, cạnh AB=4,BC=5. Quay ∆ A B C quanh AB được khối nón có thể tích V 1 , quay ∆ A B C quanh AC được khối nón có thể tích V 2 thì:
A. V 1 = V 2 = 12 π
B. V 1 > V 2
C. V 1 = V 2 = 16 π
D. V 1 < V 2