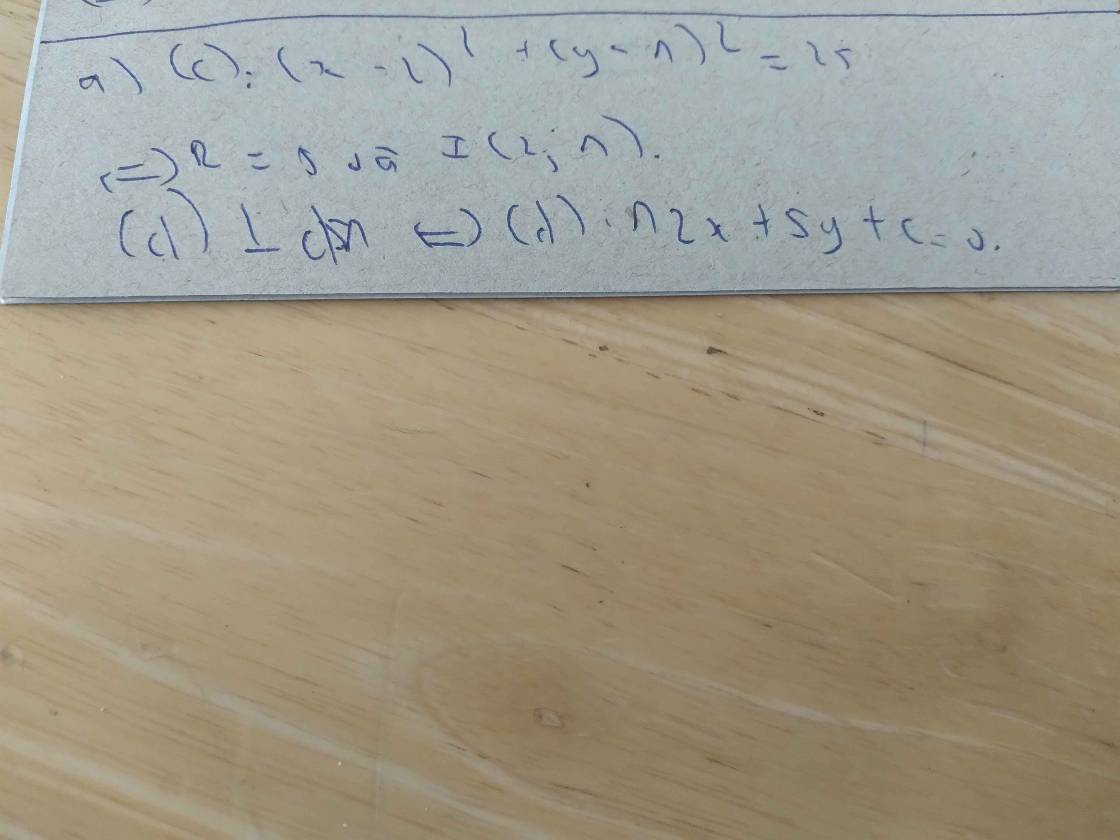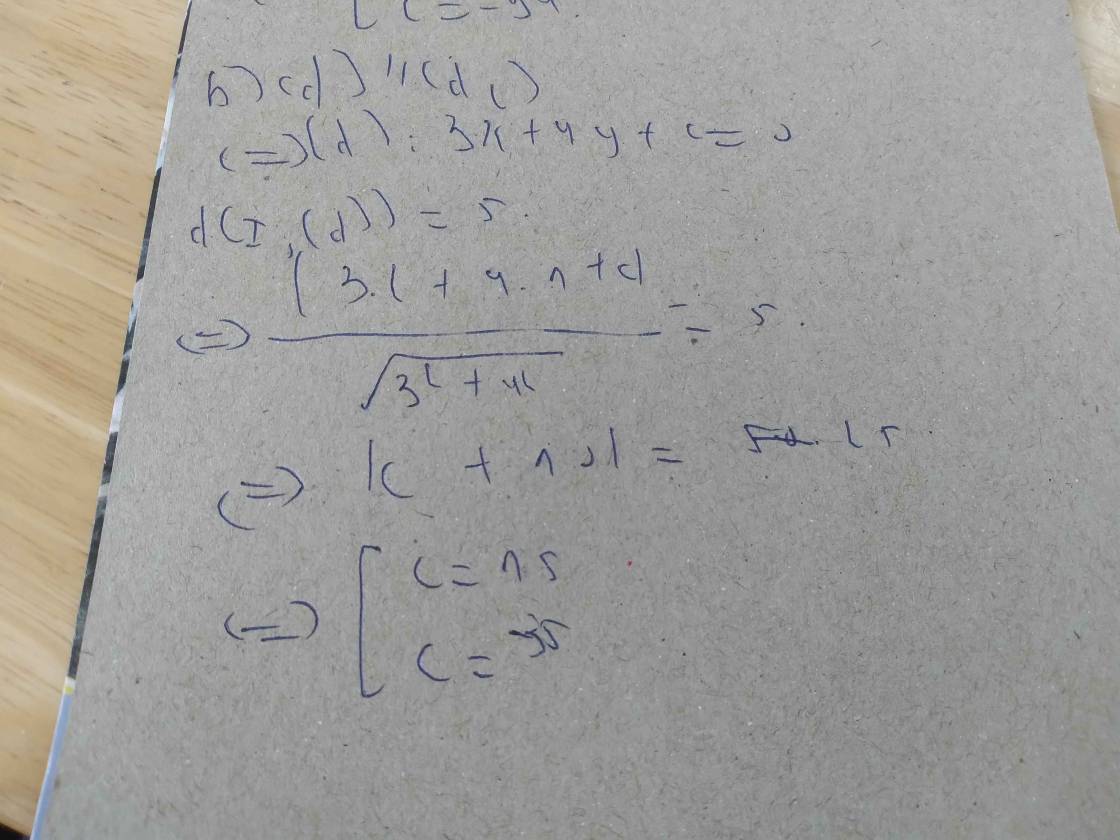\(y'=\dfrac{-4}{\left(x-1\right)^2}\)

a. \(\dfrac{2x+2}{x-1}=-2\Rightarrow2x+2=-2x+2\Rightarrow x=0\Rightarrow y'\left(0\right)=-4\)

Phương trình tiếp tuyến: \(y=-4\left(x-0\right)-2\)

b. Tiếp tuyến song song đường thẳng đã cho nên có hệ số góc k=-4

\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-2\\x=2\Rightarrow y=6\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4\left(x-0\right)-2\\y=-4\left(x-2\right)+6\end{matrix}\right.\)

c. Gọi \(M\left(x_0;y_0\right)\) là tọa độ tiếp điểm

Pt tiếp tuyến qua M có dạng: \(y=\dfrac{-4}{\left(x_0-1\right)^2}\left(x-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)

Do tiếp tuyến qua A nên:

\(3=\dfrac{-4}{\left(x_0-1\right)^2}\left(4-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)

\(\Leftrightarrow x_0^2-10x_0+21=0\Rightarrow\left[{}\begin{matrix}x_0=3\Rightarrow y'\left(3\right)=-1;y\left(3\right)=4\\x_0=7;y'\left(7\right)=-\dfrac{1}{9};y\left(7\right)=\dfrac{8}{3}\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-\dfrac{1}{9}\left(x-7\right)+\dfrac{8}{3}\end{matrix}\right.\)

d.

Do tiếp tuyến tạo với 2 trục tọa độ 1 tam giác vuông cân nên có hệ số góc bằng 1 hoặc -1

\(\Rightarrow\left[{}\begin{matrix}\dfrac{-4}{\left(x-1\right)^2}=1\left(vô-nghiệm\right)\\\dfrac{-4}{\left(x-1\right)^2}=-1\end{matrix}\right.\)

\(\Rightarrow\left(x-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=3\Rightarrow y=4\\x=-1\Rightarrow y=0\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn:

\(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-1\left(x+1\right)+0\end{matrix}\right.\)

a: \(f'\left(x\right)=\dfrac{\left(2x+2\right)'\cdot\left(x-1\right)-\left(2x+2\right)\cdot\left(x-1\right)'}{\left(x-1\right)^2}\)

\(=\dfrac{2\left(x-1\right)-2x-2}{\left(x-1\right)^2}=\dfrac{-4}{\left(x-1\right)^2}\)

y-y0=f'(x0)*(x-x0)

=>y=y0+f'(x0)*(x-x0)=f(x0)+f'(x0)(x-x0)

(d)//-4x+8 nên f(x0)=-4

=>2x+2=-4x+4

=>6x=2

=>x=1/3

f'(1/3)=-4/(1/3-1)^2=-9

y=-4+(-9)(x-1/3)=-4-9x+3=-9x-1

b: (d) vuông góc y=4x+3

=>(d): y=-1/4x+b

(d): y=f(x0)+f'(x0)*(x-x0)

=>f(x0)=-1/4

=>2x+2=-1/4(x-1)=-1/4x+1/4

=>9/4x=-7/4

=>x=-7/9

f'(-7/9)=-4/(-7/9-1)^2=-81/64

y=f(-7/9)+f'(-7/9)*(x+7/9)

=-1/4-81/64(x+7/9)

=-81/64x-79/64

a/

\(y'=-\frac{4}{\left(x-2\right)^2}\Rightarrow\left\{{}\begin{matrix}y'\left(3\right)=-4\\y\left(3\right)=6\end{matrix}\right.\)

Pt tiếp tuyến: \(y=-4\left(x-3\right)+6\Leftrightarrow y=-4x+18\)

b.

\(y'=\frac{-5}{\left(x-1\right)^2}\)

Tiếp tuyến song song với \(y=-5x-3\) nên có hệ số góc \(k=-5\)

\(\Rightarrow\frac{-5}{\left(x-1\right)^2}=-5\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)

Có 2 tiếp tuyến thỏa mãn

a:Sửa đề: y=x^3-3x^2+2

y'=3x^2-3*2x=3x^2-6x

y=2

=>x^3-3x^2=0

=>x=0 hoặc x=3

=>y'=0 hoặc y'=3*3^2-6*3=27-18=9

A(0;2); y'=0; y=2

Phương trình tiếp tuyến có dạng là;

y-2=0(x-0)

=>y=2

A(3;2); y'=9; y=2

Phương trình tiếp tuyến có dạng là:

y-2=9(x-3)

=>y=9x-27+2=9x-25

b: Tiếp tuyến tại M song song với y=6x+1

=>y'=6

=>3x^2-6x=6

=>x^2-2x=2

=>x=1+căn 3 hoặc x=1-căn 3

=>y=0 hoặc y=0

M(1+căn 3;0); y=0; y'=6

Phương trình tiếp tuyến là:

y-0=6(x-1-căn 3)=6x-6-6căn3

M(1-căn 3;0); y=0; y'=6

Phương trình tiếp tuyến là:

y-0=6(x-1+căn 3)

=>y=6x-6+6căn 3

a. y''= \(\dfrac{4}{\left(x+1\right)^3}\)

Chọn đáp án A

\(\left(C\right):\left(x-2\right)^2+\left(y-1\right)^2=25\)

\(\Rightarrow\left(C\right)\) có tâm \(I\left(2;1\right)\) ; Bán kính \(R=5\)

\( \left(C\right)//d:5x-12y+67=0\)

nên \(\Delta:5x-12y+m=0\left(m\ne67\right)\)

Vì \(d\) có \(VTPT\overrightarrow{n}=\left(5;-12\right)\) cũng là \(VTPT\) của \(\Delta\)

\(R=d\left(I,\Delta\right)=\dfrac{\left|5x_I-12y_I+m\right|}{\sqrt{5^2+\left(-12\right)^2}}\Leftrightarrow\dfrac{\left|5.2-12.1+m\right|}{13}=5\)

\(\Leftrightarrow\left|-2+m\right|=65\)

\(\Leftrightarrow\left[{}\begin{matrix}-2+m=65\\-2+m=-65\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=67\left(ktm\right)\\m=-63\left(tm\right)\end{matrix}\right.\)

Vậy pt tiếp tuyến là \(5x-12y-63=0\)

(x-2)^2+(y-1)^2=25

=>R=5; I(2;1)

(d')//(d) nên (d'): 5x-12y+c=0

Theo đề, ta có; d(I;(d'))=5

=>\(\dfrac{\left|5\cdot2+\left(-12\right)\cdot1+c\right|}{\sqrt{5^2+12^2}}=5\)

=>|c-2|=65

=>c=67 hoặc c=-63