Cho hình 43. Chứng minh rằng AI = IM.
Những câu hỏi liên quan
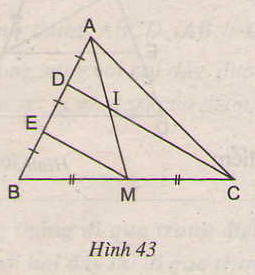
Cho hình 43. Chứng minh rằng AI = IM.
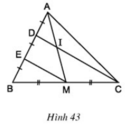
ΔBDC có BE = ED và BM = MC
⇒ EM là đường trung bình của ΔBDC
⇒ EM // DC hay EM // DI.
ΔAEM có DI // EM (cmt) và AD = DE (gt)
⇒ IA = IM (Theo định lý 1)
Đúng 0
Bình luận (0)
Chứng minh rằng AI = IM : Hình 43 SGK Toán 8
cho hình 43.Chứng minh rằng AI=IM
△BDC có ED = EB
MB = MC
⇒ EM là đường trung bình của tam giác này (Theo định nghĩa: đoạn thẳng nối trung điểm hai cạnh của một tam giác là đường trung bình của tam giác đó) ⇒ ME//CD
△AME có DA = DE (gt)
DI//ME (cmt)
⇒ IA = IM (Theo định lí: đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ 3)
Đúng 0
Bình luận (0)
\(\Delta BDC\) có BE=ED và BM=MC
nên EM// CD
\(\Rightarrow DI//EM\)
\(\Delta AEM\) có AD=DE và DI//EM
nên AI//IM
Đúng 0
Bình luận (0)
Cho hình 43. Chứng minh AI = IM ?
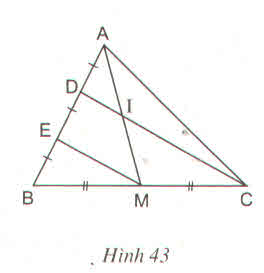
∆BDC có BE = ED và BM = MC
nên EM // DC
==> DI // EM
∆AEM có AD = DE và DI // EM
==> AI = IM.
Đúng 0
Bình luận (0)
Trong tam giác BAC có: EM là ĐTB nên DC // EM
ta có: I ∈ DC => DI // EM (DC // EM)
=> I là TĐ của AM nên AI = IM
Đúng 0
Bình luận (0)
chứng minh rằng ai = im
∆BDC có BE = ED và BM = MC
nên EM // DC
Suy ra DI // EM
∆AEM có AD = DE và DI // EM
nên AI = IM.
Đúng 0
Bình luận (8)
Cho tam giác ABC. Qua trung điểm M của cạnh BC kẻ đường thẳng song song với AB, cắt AC tại N. Trên tia BA lấy điểm I sao cho BI = MN. Chứng minh rằng IM song song với AC
(Ai vẽ hình mình tick cho nha)
TA CÓ:
IM là cạnh chung
BI=MN(gt)
góc MIB=góc IMN (AB//MN)
TAM giác IBM=Tam giác INM(c-g-c)
góc BMI=góc MIN
suy ra IM//AC
Cho tam giác ABC cân tại A. Kẻ ( ).a) Chứng minh tam giác AKH là tam giác cânb) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .c) Chứng minh: .HK song song BC
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ ( ).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .
c) Chứng minh: .HK song song BC
Cho tam giác ABC cân tại A. Kẻ ( ). a) Chứng minh tam giác AKH là tam giác cânb) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .c) Chứng minh: .HK song song BC
Đọc tiếp
Cho tam giác ABC cân tại A. Kẻ ( ).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của .
c) Chứng minh: .HK song song BC
Cho tam giác ABC, điểm D thuộc cạnh AC sao cho . Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh rằng AI = IM.
Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).
Đúng 1
Bình luận (1)