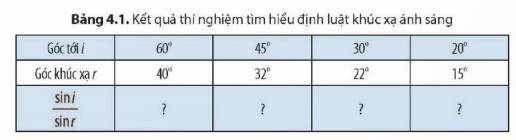
Hoàn thành Bảng 4.1, từ đó nêu nhận xét về tỉ số \(\frac{{\sin i}}{{\sin r}}\)khi góc tới thay đổi.
Hình 2 biểu diễn các số hạng của dãy số \(\left( {{u_n}} \right),\) với \({u_n} = \frac{1}{n}\) trên hệ trục tọa độ.

a) Nhận xét về sự thay đổi các giá trị \({u_n}\) khi n ngày càng lớn.
b) Hoàn thành bảng và trả lời câu hỏi sau:

Kể từ số hạng \({u_n}\) nào của dãy số thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001? 0,0001?
a) Khi n ngày càng lớn thì các giá trị \({u_n}\) ngày càng giảm tiến dần về gần trục Ox.
b)

Kể từ số hạng \({u_{1001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,001
Kể từ số hạng \({u_{10001}}\) trở đi thì khoảng cách từ \({u_n}\) đến 0 nhỏ hơn 0,0001
Dựa vào bảng số liệu (trang 17 SGK) nêu nhận xét về sự thay đổi trong sử dụng lao động theo các thành phần kỉnh tế ở nước ta và ý nghĩa của sự thay đổi đó.
- Từ năm 1985 đến năm 2002 cơ cấu sư dụng lao động theo thành phần kinh tế ở nước ta có sự chuyển biến theo hướng: tỉ lệ lao động ở khu vực Nhà nước giảm từ 15,0% (năm 1985) xuống còn 9,6% (năm 2002); tỉ lệ lao động ở các khu vực kinh tế khác tăng, từ 85,0% (năm 1985) lên 90,4% (năm 2002).
- Sự thay đổi đó thể hiện nền kinh tế nước ta đang chuyển sang thị trường và hội nhập với quốc tế
Trong hiện tượng khúc xạ ánh sáng xảy ra ở mặt phân cách giữa hai môi trường trong suốt nhất định, sin góc tới (sini) và sin góc khúc xạ (sin r ) luôn thỏa mãn hệ thức A. sin sin i r = hằng số. B. sin sin i r − = hằng số. C. sin i sin r = hằng số. D. sin sin i r + = hằng số.
Từ bảng 16.3 (SGK), hãy so sánh và cho nhận xét vẻ sự thay đổi tỉ trọng dân số thành thị, nông thôn.
- Tỉ lệ dân thành thị và nông thôn đang có sự chuyển dịch đáng kể theo hướng dân nông thôn giảm, dân thành thị tăng: năm 1990, dân thành thị là 19,5%, dân nông thôn 80,5%; đến năm 2005, dân thành thị tăng lên 27,0%, dân nông thôn giảm xuống còn 73%.
- Xu hướng phát triển phù hợp với quá trình công nghiệp hoá, hiện đại hoá.
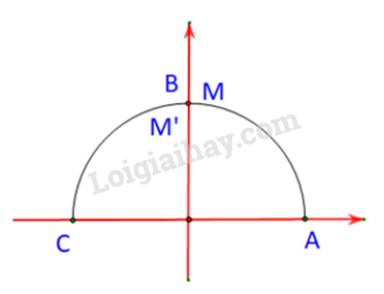
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa \(\sin \alpha \) và \(\sin \left( {{{180}^o} - \alpha } \right)\), giữa \(\cos \alpha \) và \(\cos \left( {{{180}^o} - \alpha } \right)\).
Tham khảo:
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc \(\alpha \) và \({180^o} - \alpha \).
Giả sử \(M\left( {{x_0};{y_o}} \right)\). Khi đó \(\cos \alpha = {x_0};\;\;\sin \alpha = {y_o}\)
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \(\alpha = {180^o} - \alpha = {90^o}\)
Tức là M và M’ lần lượt trùng nhau và trùng với B.
Và \(\left\{ \begin{array}{l}\cos \alpha = - \cos \left( {{{180}^o} - \alpha } \right) = 0;\\\sin \alpha = \sin \left( {{{180}^o} - \alpha } \right) = \sin {90^o} = 1.\\\cot \alpha = 0\end{array} \right.\)
Không tồn tại \(\tan \alpha \) với \(\alpha = {90^o}\)
Trường hợp 2: \(\alpha < {90^o} \Rightarrow {180^o} - \alpha > {90^o}\)
M nằm bên phải trục tung
M’ nằm bên trái trục tung
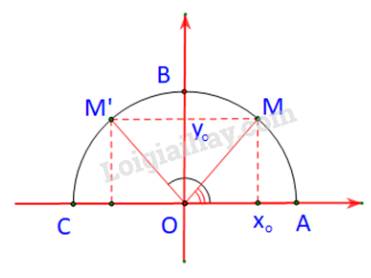
Dễ thấy: \(\widehat {M'OC} = {180^o} - \widehat {xOM'} = {180^o} - \left( {{{180}^o} - \alpha } \right) = \alpha = \widehat {xOM}\)
\( \Rightarrow \widehat {M'OB} = {90^o} - \widehat {M'OC} = {90^o} - \widehat {MOA} = \widehat {MOB}\)
Xét tam giác \(M'OB\) và tam giác \(MOB\) ta có:
\(OM = OM'\)
\(\widehat {M'OB} = \widehat {MOB}\)
OB chung
\(\begin{array}{l} \Rightarrow \Delta MOB = \Delta M'OB\\ \Rightarrow \left\{ \begin{array}{l}OM = OM'\\BM = BM'\end{array} \right.\end{array}\)
Hay OB là trung trực của đoạn thẳng MM’.
Nói cách khác M và M’ đối xứng với nhau qua trục tung.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(M'\left( { - {x_0};{y_o}} \right)\)
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Trường hợp 3: \(\alpha > {90^o} \Rightarrow {180^o} - \alpha < {90^o}\)
Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.
Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.
Như vậy
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Kết luận: Với mọi \({0^o} < \alpha < {180^o}\), ta luôn có
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha .\\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \;\;\;(\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array}\)
Một chùm tia sáng hẹp truyền từ môi trường (1) chiết suất n1 tới mặt phẳng phân cách với môi trường (2) chiết sất n2. Cho bết n1 < n2 và i có giá trị thay đổi. Trường hợp nào sau đây có hiện tượng phản xạ toàn phần?
A. Chùm tia sáng gần như sát mặt phẳng phân cách.
B. Góc tới i thỏa mãn điều kiện sin i > \(\frac{n_{1}}{n_{2}}\)
C. Góc tới i thỏa mãn điều kiện sin i <\(\frac{n_{1}}{n_{2}}\)
D. Không trường hợp nào đã nêu.
Cho hàm số \(y = \sin x\).
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị sau của hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) bằng cách tính giá trị của \(\sin x\) với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của \(\sin x\) với những x âm.
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm \(M\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = 2\pi \), ta được đồ thị của hàm số \(y = \sin x\) như hình dưới đây.
Từ đồ thị ở Hình 1.14, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số \(y = \sin x\)
a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) = - \sin x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \sin x\) là hàm số lẻ.
b)
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\sin x\) | \(0\) | \( - \frac{{\sqrt 2 }}{2}\) | \( - 1\) | \( - \frac{{\sqrt 2 }}{2}\) | 0 | \(\frac{{\sqrt 2 }}{2}\) | 1 | \(\frac{{\sqrt 2 }}{2}\) | 0 |
c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)
Một tia sáng chiếu xiên góc từ một môi trường sang môi trường chiết quang kém hơn với góc tới i thì tia khúc xạ hợp với pháp tuyến một góc khúc xạ r. Khi tăng góc tới i ( Với sin i < n 2 n 1 ) thì góc khúc xạ r
A. tăng lên và r > i.
B. tăng lên và r < i.
C. giảm xuống và r > i.
D. giảm xuống và r < i.
Dựa vào bảng 8.2 và hình 8.3, hãy nhận xét sự thay đổi của dân số LB Nga và nêu hệ quả của sự thay đổi đó.
Dân số sụt giảm, tỉ suất gia tăng dân số tự nhiên âm.
Thiếu lực lượng lao động (kể cả nguồn lao động bổ sung).
Câu 1: Lập bảng số liệu cơ cấu các nhóm tuổi của nước ta năm 1989 và năm 1999 (Đơn vị: %). Nêu nhận xét sự thay đổi tỉ lệ dân số phụ thuộc từ năm 1989 đến 1999.