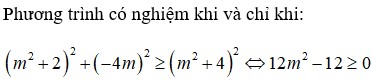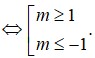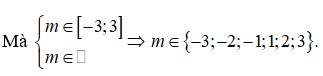Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0;2024) để \(lim\sqrt{\dfrac{9^n+3^{n+1}}{5^n+9^{n+a}}}\le\dfrac{1}{2187}\)?

Những câu hỏi liên quan
Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0; 2019) để
l
i
m
9
n
+
3
n
+
1
5
n
+
9...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0; 2019) để l i m 9 n + 3 n + 1 5 n + 9 n + a ≤ 1 2187 ?
A. 2011
B. 2018
C. 2019
D. 2012
Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0;2019) để
l
i
m
9
n
+
3
n
+
1
5
n
+
9...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0;2019) để l i m 9 n + 3 n + 1 5 n + 9 n + a ≤ 1 2187 ?
A. 2018.
B. 2011.
C. 2012.
D. 2019.
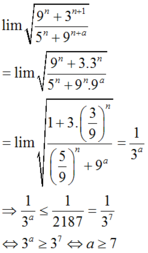
Kết hợp điều kiện đề bài
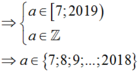
Vậy có 2018 - 7 + 1 = 2012 giá trị của a thỏa mãn.
Chọn C.
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-2017;2017] để hàm số
y
x
3
−
6
x
2
+
m
x
+
1
đồng biến trên khoảng
0
;
+
∞
A. 2030 B. 2005 C. 2018 D. 2006
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-2017;2017] để hàm số y = x 3 − 6 x 2 + m x + 1 đồng biến trên khoảng 0 ; + ∞
A. 2030
B. 2005
C. 2018
D. 2006
Đáp án D

giá trị nguyên của tham số m cần tìm
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
m
x
4
-
m
-
5
x
2
-
3
đồng biến trên khoảng (0;+¥). A. 6 B. 4 C. 3 D. 5
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số y = m x 4 - m - 5 x 2 - 3 đồng biến trên khoảng (0;+¥).
A. 6
B. 4
C. 3
D. 5
Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-281;2018] để hàm số
y
x
3
-
6
x
2
+
m
x
+
1
đồng biến trên khoảng (1;+∞). A. 2007. B. 2030. C. 2005. D. 2018.
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [-281;2018] để hàm số y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng (1;+∞).
A. 2007.
B. 2030.
C. 2005.
D. 2018.
1.Cho phương trình x2 +4x-m=0(1).Tìm tất cả các giá trị của tham số m để phương trinh (1) có đúng 1 nghiệm thuộc khoảng (-3,1)
2.Có bao nhiêu giá trị m nguyên trong nửa khoảng (0;2019] để phương trình |x2 -4|x|-5|-m có hai nghiệm phân biệt
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình x4-2x2+3-2m=0 có nghiệm thuộc (-2;2) ?
- Đặt \(a=x^2\left(a\ge0\right)\)
PTTT \(a^2-2a-2m+3=0\)
Có : \(\Delta^,=\left(-1\right)^2-\left(-2m+3\right)=1+2m-3=2m-2\)
- Theo viet : \(\left\{{}\begin{matrix}a_1+a_2=2\\a_1a_2=3-2m\end{matrix}\right.\)
- Để phương trình đề có nghiệm :
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta^,\ge0\\a_1+a_2>0\\a_1a_2\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m-2\ge0\\3-2m\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m\le\dfrac{3}{2}\end{matrix}\right.\)
\(\Rightarrow1\le m\le\dfrac{3}{2}\) ( * )
- Lại có : \(x^4-2x^2=3-2m\)
- Đặt \(f\left(x\right)=x^4-2x^2\)
- Ta có đồ thị của hàm số :
- Theo đồ thị hàm số để phương trình có nghiệm thuộc ( -2; 2 )
\(\Leftrightarrow-1\le3-2m\le8\)
\(\Leftrightarrow-\dfrac{5}{2}\le m\le2\) ( ** )
- Kết hợp điều kiện ( * ) và ( ** ) ta được : \(m\in\left[1;\dfrac{3}{2}\right]\)
Vậy có 1 giá trị m thỏa mãn điều kiện đề bài ( m = 1 ) .
Đúng 1
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=|3x⁴-mx³+6x²+m-3| đồng biến trên khoảng (0- dương vô cùng)
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình
(
m
2
+
2
)
c
o
s
2
x
-
2
m
sin
2
x
+
1
0
có nghiệm A. 3 B. 7 C. 6 D. 4
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình ( m 2 + 2 ) c o s 2 x - 2 m sin 2 x + 1 = 0 có nghiệm
A. 3
B. 7
C. 6
D. 4
Cho hàm số
f
(
x
)
m
x
4
+
2
x
2
-
1
với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m thuộc khoảng (-2018;2018) sao cho hàm số đã cho đồng biến trên khoảng (0;1/2)? A.2022...
Đọc tiếp
Cho hàm số f ( x ) = m x 4 + 2 x 2 - 1 với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m thuộc khoảng (-2018;2018) sao cho hàm số đã cho đồng biến trên khoảng (0;1/2)?
A.2022
B.4032
C.4
D.2014
Chọn D
![]() .
.
![]() :
: ![]() Hàm số đồng biến trên
Hàm số đồng biến trên ![]()
![]() thỏa mãn.
thỏa mãn.
![]() :
:
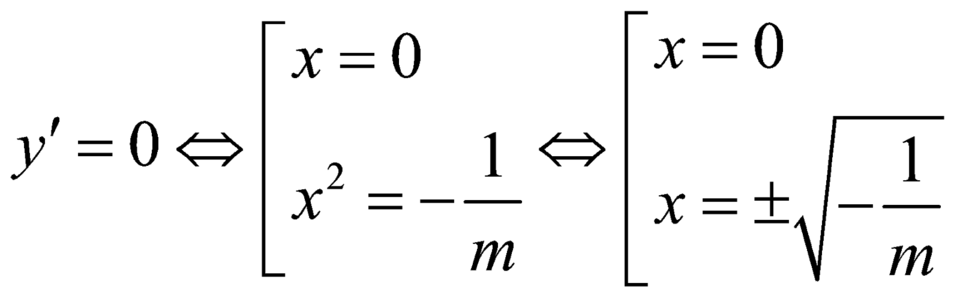 .
.
BBT :

Dựa vào BBT, hàm số đồng biến trên khoảng
![]()
![]()
![]() .
.
So với điều kiện ![]() .
.
Mặt khác, theo giả thiết 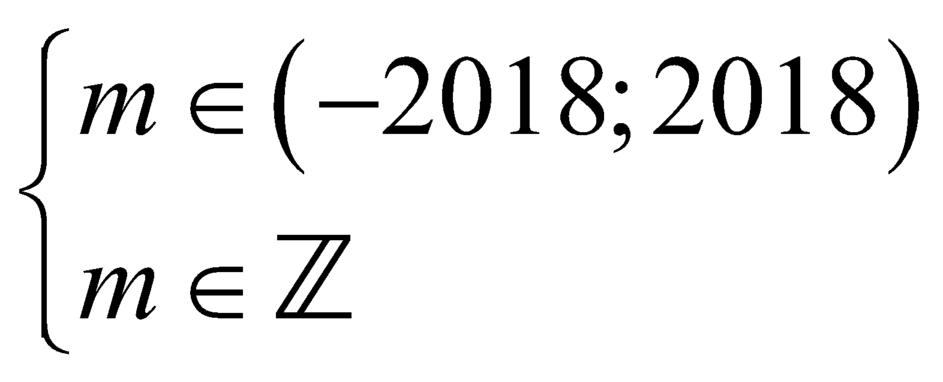
suy ra có ![]() giá trị nguyên của
giá trị nguyên của ![]() thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)