em chỉ cần hình thôi ạ

giúp em các bài 10,13,20 với mn ơi em chỉ cần trình bày thôi ạ nếu có hình vẽ thì càng tốt ạ
em chỉ cần bài văng bình thường thôi ạ không cần dài quá đâu ạ em cảm ơn
Chỉ cần vẽ hình thôi ạ ko cần giải
\(a,\) Vì AH la đường cao tg ABC cân A nên AH cũng là trung tuyến
Mà H là trung điểm AE nên ABEC là hbh
Mà AE vuông BC tại H nên ABEC là hthoi
\(b,\) Theo tc trung tuyến ứng cạnh huyền thì \(HI=\dfrac{1}{2}AC\)
Vì D,F là trung điểm AH,HC nên DF là đtb
Do đó \(DF=\dfrac{1}{2}AC\)
Vậy \(DF=HI\)
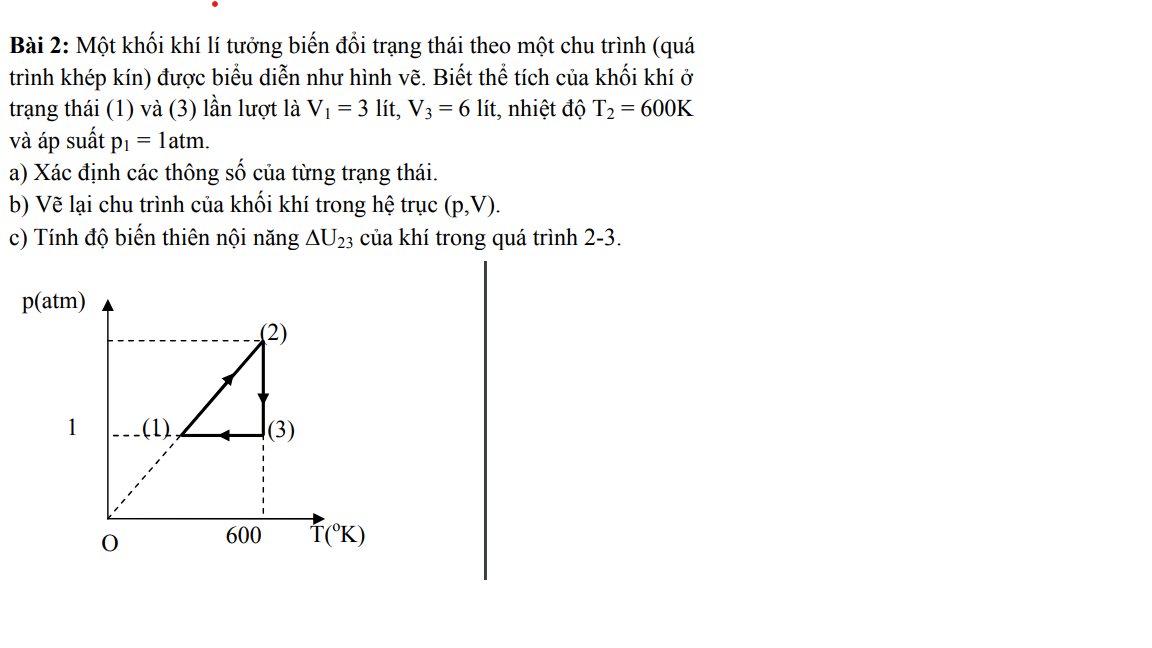
Dạ em chỉ cần câu c thôi ạ, mọi người giúp em với ạ
chỉ cần làm câu 7,8,9 thôi ạ giúp em với ạ

Minh is going to watch cartoon on TV tonight.
What does Lan look like? (Lan trông như thế nào? - hỏi về ngoại hình)
What is Hoang like? (Hoàng là người như thế nào? - hỏi về tính cách)
Giúp mik bài này vs ạ, chỉ cần cậ d thôi ạ( mn giúp em vs em đang cần gấp )
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
Em chỉ cần phần c thôi ạ
\(A=\dfrac{1}{200\cdot199}-\dfrac{1}{199\cdot198}-\dfrac{1}{198\cdot197}-...-\dfrac{1}{3\cdot2}-\dfrac{1}{2\cdot1}\)
\(=\dfrac{1}{199}-\dfrac{1}{200}-\left(1-\dfrac{1}{2}-...+\dfrac{1}{198}-\dfrac{1}{199}\right)\)
\(=\dfrac{1}{199}-\dfrac{1}{200}-1+\dfrac{1}{199}\)
\(=\dfrac{-39599}{39800}\)
\(\dfrac{1}{200.199}-\dfrac{1}{199.198}-\dfrac{1}{198.197}-...-\dfrac{1}{3.2}-\dfrac{1}{2.1}\)
\(=-\left(\dfrac{1}{200.199}+\dfrac{1}{199.198}+\dfrac{1}{198.197}+...+\dfrac{1}{3.2}+\dfrac{1}{2.1}\right)=-\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{197.198}+\dfrac{1}{198.199}+\dfrac{1}{199.200}\right)=-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{197}-\dfrac{1}{198}+\dfrac{1}{198}-\dfrac{1}{199}+\dfrac{1}{199}-\dfrac{1}{200}\right)=-\left(1-\dfrac{1}{200}\right)=\dfrac{1}{200}-1=-\dfrac{199}{200}\)
Em chỉ cần đáp án thôi ạ
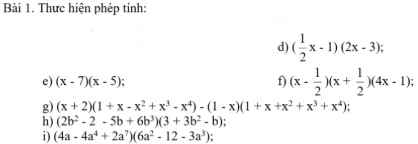
d: \(\left(\dfrac{1}{2}x-1\right)\left(2x-3\right)\)
\(=x^2-\dfrac{3}{2}x-2x+3\)
\(=x^2-\dfrac{7}{2}x+3\)
e: Ta có: \(\left(x-7\right)\left(x-5\right)\)
\(=x^2-5x-7x+35\)
\(=x^2-12x+35\)
f: Ta có: \(\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)\left(4x-1\right)\)
\(=4\left(x-\dfrac{1}{4}\right)\left(x-\dfrac{1}{4}\right)\)
\(=4\left(x-\dfrac{1}{4}\right)^2\)
\(=4\left(x^2-\dfrac{1}{2}x+\dfrac{1}{16}\right)\)
\(=4x^2-2x+\dfrac{1}{4}\)
Chỉ cần vẽ hình bài này thôi ạ

Giải giúp em cậu này với ạ chỉ cần câu hs thôi ạ
Câu 1:
1:
a: \(\dfrac{1}{2}x-3=0\)
=>\(\dfrac{1}{2}x=3\)
=>\(x=3:\dfrac{1}{2}=3\cdot2=6\)
b: \(3x^2-12x=0\)
=>\(3x\cdot x-3x\cdot4=0\)
=>\(3x\left(x-4\right)=0\)
=>x(x-4)=0
=>\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
2:
a: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=-x+\dfrac{3}{2}\)
=>\(x^2=-2x+3\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Khi x=-3 thì \(y=\dfrac{1}{2}\cdot\left(-3\right)^2=\dfrac{1}{2}\cdot9=4,5\)
Khi x=1 thì \(y=\dfrac{1}{2}\cdot1^2=\dfrac{1}{2}\)
b: Gọi (d1): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Thay x=2 và y=2 vào (d), ta được:
\(a\cdot2+b=2\)
=>2a+b=2
=>b=2-2a
=>y=ax+2-2a
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2=ax+2-2a\)
=>\(\dfrac{1}{2}x^2-ax-2+2a=0\)
\(\text{Δ}=\left(-a\right)^2-4\cdot\dfrac{1}{2}\cdot\left(2a-2\right)\)
\(=a^2-2\left(2a-2\right)=a^2-4a+4=\left(a-2\right)^2\)
Để (P) tiếp xúc với (d1) thì Δ=0
=>a-2=0
=>a=2
=>b=2-2a=2-4=-2
Vậy: Phương trình đường thẳng cần tìm là y=2x-2