cho t/g ABC có góc B=120 độ AB=6, \(\dfrac{AB+AC}{2}=BC\) tính diện tích ABC

Những câu hỏi liên quan
cho t/g ABC có góc B=120 độ AB=6, \(\dfrac{AB+AC}{2}=BC\) tính diện tích ABC
Cho tam giác ABC,góc B= 120 độ,BC=12,AB=6.Phân giác góc B cắt AC tại D. Tính diện tích ABd
Cho tam giác abc với các đường cao ah, biết góc abc=120, ab=6,25cm, bc=12,5cm. Đường phân giác của góc b cắt ac tại d.
a) Tính độ dài bd
b) Tính tỷ số diện tích của tam giác abd và abc
c) Tính diện tích của tam giác ABD
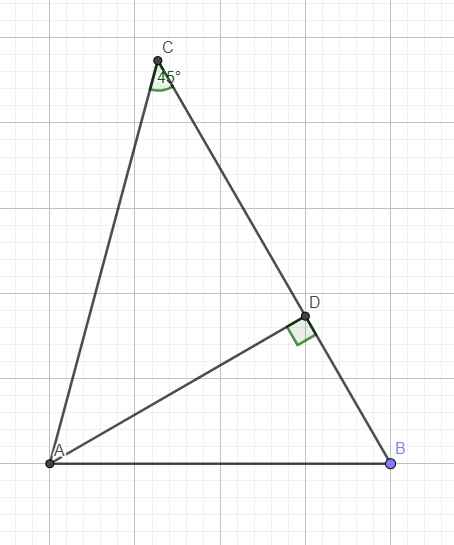
Cho tam giác ABC có góc C bằng 45 độ, AB. AC=32\(\sqrt{6}\), AB:AC=\(\sqrt{6}\):3. Tính BC, góc B và diện tích tam giác ABC
\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)
Đúng 0
Bình luận (0)
cho tam giác có góc C = 45 độ . AB nhân AC = 32 căn 6; AB chia AC = căn 6 chia 3 . tính số đo cạnh BC; góc B và diện tích tam giác ABC
Xin chào bạn. Rất vui đc làm quen với bạn. Chúc bạn chăm chỉ học tập như hiện tại nhé!!
Đúng 0
Bình luận (0)
cho tam giác ABC có góc B=120 độ,AB=6,25cm,BC=2XAB.Đường phân giác của góc Bcát AC tại D
a,Tính đọ dài AD
b,Tính diện tích tam giác ABD
cho tam giác abc có góc a bằng 120 độ, góc b bằng 40 độ, kẻ các đường phân giác trong ad,be.a) chứng minh rằng 1/ab+1/ac=1/ad b) cho ab=m, ac=n ,diện tích tam giác abc là s tính diện tích tam giác abe theo m,n,s
Cho tam giác ABC có AB = 16cm, AC = 14cm, góc B = 40 độ. Tính BC và diện tích tam giác ABC
cosB=(16^2+BC^2-14^2)/(2*16*BC)
=>BC^2+60=32*BC*cos40
=>BC=21,76cm
S ABC=1/2*21,76*16*sin40=111,90cm2
Đúng 0
Bình luận (0)
Cho∆ ABC có AC = 8 và góc A =120° . Trên đoạn AB lấy điểm M sao cho AM = 2/3 AB . Biết diện tích ∆BMC =4√3 . Tính độ dài cạnh AB .
AM=2/3AB
=>BM=1/3AB
=>\(\dfrac{S_{BMC}}{S_{BAC}}=\dfrac{1}{3}\)
=>\(S_{BAC}=3\cdot S_{BMC}=12\sqrt{3}\)
\(\Leftrightarrow\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=12\sqrt{3}\)
=>\(\dfrac{1}{2}\cdot8\cdot AB\cdot sin120=12\sqrt{3}\)
=>\(AB\cdot2\sqrt{3}=12\sqrt{3}\)
=>AB=6
Đúng 1
Bình luận (0)
Cho tam giác ABC, góc B là 120 độ ,AB=6,AC=14.Tính độ dài BC