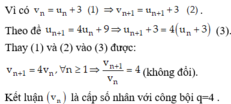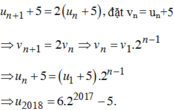Cho dãy số xác định bởi u1 = 1; \(u_{n+1}=\dfrac{1}{3}\left(2u_n+\dfrac{n-1}{n^2+3n+2}\right)\). Khi đó \(u_{2030}\) là

Những câu hỏi liên quan
Cho dãy số
u
n
được xác định bởi
u
1
2
u
n
+
1...
Đọc tiếp
Cho dãy số u n được xác định bởi u 1 = 2 u n + 1 = 4 u n + 9
Dãy số v n xác định bởi v n = u n + 3 , với mọi n ≥ 1 . Khẳng định nào dưới đây đúng?
A. Dãy v n là cấp số cộng với công sai d=3 .
B. Dãy v n là cấp số nhân với công bội q=4.
C. Dãy v n là cấp số cộng với công sai d=4 .
D. Dãy v n là cấp số nhân với công bội q= 9
1) cho dãy số (un)(��) được xác định bởi unn^2-1�3�−1a) Tính u1,u2,u3,u4b) 99 là số hạng thứ mấy của dãy2) cho dãy số (un)(��) được xác định bởi u_ndfrac{2n-1}{n+1}a) Tính u1,u2,u3,u4b) dfrac{13}{7} là số hạng thứ mấy của dãy
Đọc tiếp
1) cho dãy số được xác định bởi
a) Tính
2) cho dãy số được xác định bởi
b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.
Đúng 0
Bình luận (0)
Cho dãy số
U
n
xác định bởi
U
1
2
U
n
u
1
+...
Đọc tiếp
Cho dãy số U n xác định bởi
U 1 = 2 U n = u 1 + u 2 + . . + n - 1 u n - 1 n n 2 - 1
Tìm l i m n + 2018 3 U n
A. 1
B. 2
C. 3
D. 4
Ta có u 2 = 1 3
Với n ≥ 3 ta có
u 1 + 2 u 2 + . . + n - 1 u n - 1 + n u n = n n 2 - 1 u n + n u n = n 3 u n ⇒ n u n 3 = n u n + n - 1 3 u n - 1 ⇒ u n u n - 1 = n - 1 3 n 3 - n = n - 1 n 2 n n + 1 1
Từ (1) suy ra
u n u 2 = u n u n - 1 . u n - 1 u n - 2 . . . u 3 u 2 = n - 1 n 2 . n - 1 n - 2 2 . . 2 3 2 n n - 1 . n - 1 n . . . 3 4 = 12 n 2 n + 1 ⇒ u n = 4 n 2 n + 1
Vậy l i m n + 2018 3 U n = 4
Đáp án D
Đúng 0
Bình luận (0)
Cho dãy số xác định bởi
u
1
1
u
n
+
1
2
u
n...
Đọc tiếp
Cho dãy số xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 Tính số hạng thứ 2018 của dãy.
A. u2018 = 3.22018 + 5
B. u2018 = 3.22017 + 1
C. u2018 = 6.22017 – 5
D. u2018 = 6.22018 - 5
Chọn D.
Ta có 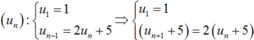
Đặt: vn = un + 5 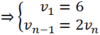
Khi đó ta được dãy mới; là cấp số nhân với : v1 = 6; q = 2
⇒ v2018 = 22017.v1 = 6.22017 ⇒ u2018 = 6.22017 – 5.
Đúng 0
Bình luận (0)
Cho dãy số
u
n
xác định bởi
u
1
1
u
n
+
1
2...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 . Tính số hạng thứ 2018 của dãy.
A. u 2018 = 3.2 2018 + 5
B. u 2018 = 3.2 2017 + 1
C. u 2018 = 6.2 2018 − 5
D. u 2018 = 6.2 2018 − 5
Đáp án D
Ta có: u n : u 1 = 1 u n − 1 = 2 u n + 5 ⇒ u 1 = 1 u n + 1 + 5 = 2 u n + 5
Đặt: v n = u n + 5 ⇒ v 1 = 6 v n − 1 = 2 v n
⇒ v 2018 = 2 2017 . v 1 = 6.2 2017 ⇒ u 2018 = 6.2 2017 − 5
Đúng 0
Bình luận (0)
Cho dãy số
u
n
xác định bởi
u
1
1
u
n
+
1
2...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 . Tính số hạng thứ 2018 của dãy.
A. u 2018 = 3.2 2018 + 5
B. u 2018 = 3.2 2017 + 5
C. u 2018 = 3.2 2018 − 5
D. u 2018 = 3.2 2017 − 5
Đáp án C
Phân tích v n + 1 + k = 2 u n + k ⇒ k = 5 ⇒ u n + 1 + 5 = 2 u n + 5
Đặt
v n = u n + 5 ⇒ v n + 1 = 2 v n C S N ⇒ v n = v 1 q n − 1 = u 1 + 5 .2 n − 1 = 6.2 n − 1
⇒ u n + 5 = 6.2 n − 1 ⇒ u 2018 = 6.2 2017 − 5
Đúng 0
Bình luận (0)
Cho dãy số
U
n
xác định bởi
U
1
1
3
và
U
n
+
1
n
+
1
3
n...
Đọc tiếp
Cho dãy số U n xác định bởi U 1 = 1 3 và U n + 1 = n + 1 3 n U n . Tổng S = U 1 + U 2 2 + U 3 3 + . . . + U 10 10 bằng
A. 3280 6561
B. 29524 59049
C. 25942 59049
D. 1 243
Cho dãy số
u
n
xác định bởi:
u
1
1
3
;
u
n
+
1
n
+
1
3
n
u
n
. Tổng
S
u
1
+
u...
Đọc tiếp
Cho dãy số u n xác định bởi: u 1 = 1 3 ; u n + 1 = n + 1 3 n u n . Tổng S = u 1 + u 2 2 + u 3 3 + . . . + u 10 10 bằng
A. 3280 6561
B. 29524 59049
C. 25942 59049
D. 1 243
Cho dãy số
u
n
xác định bởi
u
1
1
u
n
+
1
2...
Đọc tiếp
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = 2 u n + 5 Tính số hạng thứ 2018 của dãy số trên
A. u 2018 = 6 . 2 2017 - 5
B. u 2018 = 6 . 2 2018 - 5
C. u 2018 = 6 . 2 2017 + 1
D. u 2018 = 6 . 2 2018 + 5
Cho dãy số
U
n
xác định bởi
U
1
1
3
và
U
n
+
1
n
+
1
3
n
U
n
.
Tổng...
Đọc tiếp
Cho dãy số U n xác định bởi U 1 = 1 3 và U n + 1 = n + 1 3 n U n . Tổng S = U 1 + U 2 2 + U 3 3 + . . . + U 10 10 bằng
A. 3280 6561
B. 29524 59049
C. 25942 59049
D. 1 243
Đáp án B
U 2 = 2 3 . 1 U 1 , U 3 = 3 3 . 2 . 2 3 . 1 U 1 , . . . , U 10 = 10 3 . 9 . 9 3 . 8 . . . 2 3 . 1 U 1 ⇒ S = U 1 + U 2 2 + U 3 3 + . . . + U 10 10 = U 1 + U 1 3 + U 1 3 3 + . . . + U 1 3 9 = U 1 1 - 1 3 10 1 - 1 3 = 29524 59049
Đúng 0
Bình luận (0)