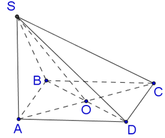
1. cho h/c đều SABCD có AB=a. Góc giữa cạnh bên và mặt đáy=45o . Tính VS.ABCD

Những câu hỏi liên quan
Tính VS.ABCD biết S.ABCD là k/c đều có cạnh đáy a, góc giữa cạnh bên và đáy 60o
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SAO}=60^0\)
\(AO=\dfrac{AC}{2}=\dfrac{1}{2}.a\sqrt{2}\)
\(\Rightarrow SO=AO.tan\widehat{SAO}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{a^3\sqrt{6}}{6}\)
Đúng 0
Bình luận (0)
Cho hình chóp đều sabcd có cạnh đáy bằng a góc giữa mặt bên và đáy là 60 độ tính thể tích sabcd
2. Cho h/c đều SABC có AB=2a.
a) Góc giữa cạnh bên và đáy = 60o. Tính VSABC
b) Góc giữa mặt bên và đáy = 30o .Tính VSABC
a: Gọi O là tâm đường tròn ngoại tiếp ΔABC
=>OA=OB=OC
mà SA=SB=SC
nên SO⊥(ABC)
\(\hat{SA;\left(ABC\right)}=60^0\)
=>\(\hat{SA;AO}=60^0\)
=>\(\hat{SAO}=60^0\)
Vì S.ABC là hình chóp đều
nên \(\hat{SA;\left(ABC\right)}=\hat{SB;\left(ABC\right)}=\hat{SBO}\)
=>\(\hat{SBO}=60^0\)
ΔABC đều có O là tâm đường tròn ngoại tiếp
nên O cũng là trọng tâm của ΔABC
Gọi H là trung điểm của AC
Xét ΔBAC đều có BH là đường trung tuyến
nên \(BH=AC\cdot\frac{\sqrt3}{2}=2a\cdot\frac{\sqrt3}{2}=a\sqrt3\)
Xét ΔBAC có
BH là đường trung tuyến
O là trọng tâm
Do đó: \(BO=\frac23BH=\frac23\cdot a\sqrt3=\frac{2a\sqrt3}{3}\)
Xét ΔSOB vuông tại O có tan SBO\(=\frac{SO}{OB}\)
=>\(SO=OB\cdot\tan60=\frac{2a\sqrt3}{3}\cdot\tan60=2a\)
Diện tích đáy là: \(S_{đáy}=\left(2a\right)^2\cdot\frac{\sqrt3}{4}=4a^2\cdot\frac{\sqrt3}{4}=a^2\sqrt3\)
=>\(V_{S.ABC}=\frac13\cdot SO\cdot S_{đáy}=\frac13\cdot2a\cdot a^2\sqrt3=\frac{2a^3\sqrt3}{3}\)
b: Gọi M là trung điểm của BC
ΔSBC cân tại S
mà SM là đường trung tuyến
nên SM⊥BC
ΔABC đều
mà AM là đường trung tuyến
nên AM⊥BC
ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\frac{\sqrt3}{2}=2a\cdot\frac{\sqrt3}{2}=a\sqrt3\)
Xét ΔABC có
AM là đường trung tuyến
O là trọng tâm
Do đó: A,O,M thẳng hàng
=>\(OM=\frac13AM=\frac{a\sqrt3}{3}\)
(SBC) giao (ABC)=BC
SM⊥BC; SM⊂(SBC)
AM⊥BC; AM⊂(ABC)
Do đó: \(\hat{\left(SBC\right);\left(ABC\right)}=\hat{SM;MA}=\hat{SMA}=\hat{SMO}\)
=>\(\hat{SMO}=30^0\)
Xét ΔSOM vuông tại O có tan M=SO/OM
=>\(SO=OM\cdot\tan M=\frac{a\sqrt3}{3}\cdot\tan30=\frac{a\sqrt3}{3}\cdot\frac{1}{\sqrt3}=\frac{a}{3}\)
Thể tích hình chóp S.BAC là:
\(V=\frac13\cdot SO\cdot S_{ABC}=\frac13\cdot\frac{a}{3}\cdot a^2\sqrt3=\frac{a^3\sqrt3}{9}\)
Đúng 0
Bình luận (0)
cho hình chóp SABCD đều cạnh đáy a, góc giữa mặt bên và đáy bằng 45°. Tính khoảng cách từ A đến (SBD)
Bạn kiểm tra lại đề, chắc là đề đúng chứ? (SBD) hay (SBC)?
Nếu đề đúng thế này thì gọi O là tâm đáy
Vì \(AC\perp BD\Rightarrow AO\perp\left(SBD\right)\Rightarrow AO=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Đúng 1
Bình luận (1)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc A bằng
60
o
,
O là tâm hình thoi, SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng
45
o
.
Tính theo a thể tích khối chóp SABCD. A.
3
2
a
3
x B.
a
3
4...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc A bằng 60 o , O là tâm hình thoi, SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng 45 o . Tính theo a thể tích khối chóp SABCD.
A. 3 2 a 3 x
B. a 3 4
C. 3 a 3 8
D. 2 a 3
Cho hình chóp đều SABCD có cạnh đáy bằng 2a,góc giữa cạnh bên và mặt phẳng đáy bằng 45°.Tính độ dài đường cao hình chóp đã cho
(SA;(ABCD))=45 độ
=>(AS;(AO)=45 độ
=>góc SAO=45 độ
AC=2a*căn 2
=>AO=a*căn 2
=>SO=a*căn 2
Đúng 0
Bình luận (0)
Cho hình chóp SABCD đều. Cạnh đáy a, góc giữa mặt bên và đáy bằng 45°. Tính khoảng cách từ a)A đến (SBD) b)O đến (SAB) c)CD đến (SAB)
Cho hình chóp tứ giác đều SABCD có cạnh đáy là a góc giữa mặt bên với mặt đáy là 60° tính khoảng cách giữa hai đường thẳng CM và SA biết M là trung điểm của SD
Bài 1. Cho hình chóp SABCD có cạnh bên SC vuông góc với đáy. Đáy ABCD là hình thoi tâm O, trong đó AABC là tam giác đều có cạnh a. Gọi H là hình chiếu vuông góc của C lên SO. Tính góc giữa SB và (ABCD)
Đề bài thiếu dữ liệu định vị điểm S (ví dụ SC bằng bao nhiêu đó) nên ko thể tính góc giữa SB và (ABCD)
Đúng 0
Bình luận (0)