cho hình thang cân ABCD có AB = 6, BC = 2 căn 2. Tính DC

Những câu hỏi liên quan
1.cho hình thoi ABCD. có góc BAD bằng 40 độ. o là giao điểm của 2 đường chéo H là hình chiếu của O trên AB trên tia dối của tia BC và DC lần lượt lấy M,N sao cho HM//AN. tính góc MON2. Cho hình vuông ABCD E là tâm của hình vuông. M là trung điểm của AB. Lấy G,H trên BC,CD sao cho MG//AH tính góc GEH3. Cho hình thang cân ABCD có đáy lớn AB bằng đường chéo AC, đáy nhỏ CDcăn 2 nhân BC.Tính các góc của hình thang ABCD
Đọc tiếp
1.cho hình thoi ABCD. có góc BAD bằng 40 độ. o là giao điểm của 2 đường chéo H là hình chiếu của O trên AB trên tia dối của tia BC và DC lần lượt lấy M,N sao cho HM//AN. tính góc MON
2. Cho hình vuông ABCD E là tâm của hình vuông. M là trung điểm của AB. Lấy G,H trên BC,CD sao cho MG//AH tính góc GEH
3. Cho hình thang cân ABCD có đáy lớn AB bằng đường chéo AC, đáy nhỏ CD=căn 2 nhân BC.Tính các góc của hình thang ABCD
Cho hình thang cân ABCD có AB // DC và AB<DC, đường chéo BD vuông góc với cạnh bên BC. Vẽ đường cao BH
a) Chứng minh △BDC đồng dạng với △HBC
b) Cho BC= 15cm, DC= 25cm. Tính HC và HD
c) Tính diện tích hình thang ABCD
a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng vói ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
Đúng 0
Bình luận (0)
1)Cho hình thang cân ABCD (AB//DC) có B=2C. Tính B,C,D
2)Cho hình thang cân ABCD (AB//DC) O là giao điểm hai đường chéo AC và BD. Chứng minh OA=ob VÀ oc=op
3)Cho tứ giác ABCD (AB nhỏ hơn DC) AH vuông BC. gọi M,N,I lần lượt là trung điểm AC,AC,BC. chứng minh:
a) MN là đường trung trực của AH
b) Chứng minh tứ giác MHIN là hình thang cân
cho tam giác ABC cân tại A có AB=căn 2 và BC = 2 . D là điểm đối xứng với A qua BC
a) tính BD,DC
b) tứ giác ABCD là hình gì ? vì sao? tính diện tích ABCD
HÃY GIÚP TÔI
Cho hình thang ABCD có AB//CD, AB<CD, đường chéo BD vuông góc với cạnh BC. Kẻ BH vuông góc với CD. Tính diện tích hình thang ABCD biết BC=15cm, DC= 25cm. (ABCD ko phải hình thang cân)
Cho hình thang cân ABCD có AB//DC và AB<DC, đường chéo BD vuông góc với cạnh bên C.Về đường cao BH. a Chứng minh ABDC đồng dạng A HBC b Cho BC=15cm DC=25. Tính HC và HD • Tính diện tích hình thang ABCD.
a:Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng với ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
Đúng 0
Bình luận (0)
Mọi người ơi giúp mk với ~ Mk cảm ơn ~
Bài 1. cho ABCD là hình thang có AD // BC, có góc A - B = 20 độ, góc D= 2. góc B. tính số đo các góc của hình thang .
Bài 2. Cho hình thang cân ABCD, AB//CD, AD=AB, BD=DC. Tính các góc của hình thang cân.
Mơn ạ ~
Bài 1: ( hình tự vẽ )
Vì \(AD//BC\left(gt\right)\)
\(\Rightarrow\widehat{A}+\widehat{B}=180^0\)( 2 góc trong cùng phía ) mà\(\widehat{A}-\widehat{B}=20^0\left(gt\right)\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=100^0\\\widehat{B}=80^0\end{cases}}\)
\(\widehat{D}=2\widehat{B}=2.80^0=160^0\)
Do \(AD//BC\left(gt\right)\)
\(\Rightarrow\widehat{D}+\widehat{C}=180^0\)( 2 góc trong cùng phía )
\(\Rightarrow\widehat{C}=20^0\)
Vậy ...
Đúng 1
Bình luận (1)
Bài 1:Cho hình thang cân ABCD ( AB// CD) có AB = 3 cm, CD = 6 cm, AD = 2,5 cm. Vẽ 2 đường cao AH, BK. Tính DH, DK, AH.
Bài 2: Cho hình thang ABCD (AB//CD) có AC = BD. Qua B kẻ đường thẳng song song vs AC, cắt đường thẳng DC tại E. Chứng minh rằng:
a) Tam giác BDE là tam giác cân.
b) Hình thang ABCD là hình thang cân.
Cho hình thang ABCD có
A
^
D
^
90
°
, DC BC 2.AB, DC 4cm. Tính góc ABC của hình thang. A.
110
°
B.
150
°
C.
120
°
D.
135
°
Đọc tiếp
Cho hình thang ABCD có A ^ = D ^ = 90 ° , DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
A. 110 °
B. 150 °
C. 120 °
D. 135 °
Đáp án cần chọn là: C
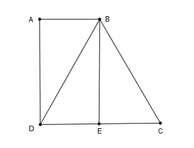
Từ B kẻ BE vuông góc với CD tại E.
Tứ giác ABED là hình thang có hai cạnh bên AD // BE nên AD = BE, AB = DE.
Mặt khác, DC = BC = 2AB nên DC = 2ED, do đó E là trung điểm của DC.
Xét ΔBDE và ΔBCE có B E D ^ = B E C ^ = 90 ° ; DE = EC
BE cạnh chung nên ΔBED = ΔBEC (c – g – c)
Suy ra BD = BC mà BC = DC (gt) => BD = BC = CD nên ΔBCD đều.
Xét ΔBCD đều có BE là đường cao cũng là đường phân giác nên
E B C ^ = 1 2 D B C ^ = 1 2 × 60 ° = 30 °
Vì AD // BE mà B A D ^ = 90 ° nên A B E ^ = 180 ° - B A D ^ = 180 ° - 90 ° = 90 ° (hai góc trong cũng phía bù nhau)
Từ đó A B C ^ = A B E ^ + E B C ^ = 90 ° + 30 ° = 120 °
Vậy A B C ^ = 120 °
Đúng 0
Bình luận (0)















