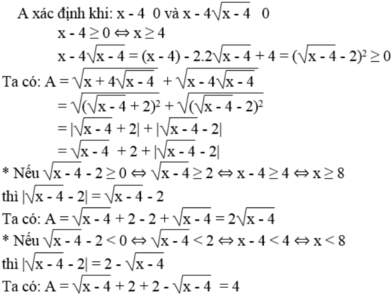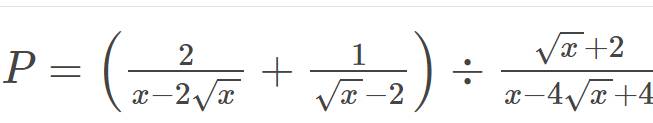 tìm điều kiện xác định và rút gọn ạaaa
tìm điều kiện xác định và rút gọn ạaaa

Những câu hỏi liên quan
Tìm điều kiện xác định và rút gọn
Tìm điều kiện xác định và rút gọn biểu thức: A = x + 4 x - 4 + x - 4 x - 4
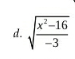 (tìm điều kiện xác định)
(tìm điều kiện xác định)
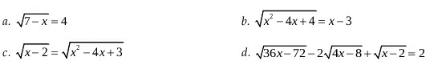 ( tìm x biết)
( tìm x biết)
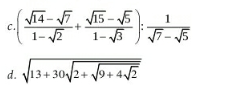 (rút gọn)
(rút gọn)
Các anh e giúp mik vs
ĐKXĐ: \(\dfrac{x^2-16}{-3}\ge0\)
vì \(-3< 0\) nên \(x^2-16\le0\Rightarrow x^2\le16\Rightarrow-4\le x\le4\)
Đúng 1
Bình luận (1)
khi rút gọn biểu thức chứa căn có tìm điều kiện xác định không
Thằng kia hỏi ngu đến thế là cùng. Học lớp mấy rồi mà còn hỏi câu này.
Đúng 0
Bình luận (1)
Hoàng Quân, mình đã nói với cậu là đừng ăn nói lung tung.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
rút gọn phân thức:\(\dfrac{\left(x^2+2x+4\right)}{x+2}\)
tìm điều kiện xác định để phân thức trên được xác định
a. Khi rút gọn biểu thức hửu tỉ có tìm điều kiện xác định không ? từ đó hãy rút gọn biểu thức M left(dfrac{1}{1+x}+dfrac{2x}{1-x^{text{2}}}right):left(dfrac{1}{x}-1right)b. Khi rút gọn biểu thức chứa căn có tìm điều kiện không ? từ đó hãy rút gọn biểu thức N dfrac{sqrt{x}+1}{sqrt{text{x}}-2}+dfrac{2sqrt{x}}{sqrt{x}+2}+dfrac{2+5sqrt{x}}{4-x}
Đọc tiếp
a. Khi rút gọn biểu thức hửu tỉ có tìm điều kiện xác định không ? từ đó hãy rút gọn biểu thức M = \(\left(\dfrac{1}{1+x}+\dfrac{2x}{1-x^{\text{2}}}\right):\left(\dfrac{1}{x}-1\right)\)
b. Khi rút gọn biểu thức chứa căn có tìm điều kiện không ? từ đó hãy rút gọn biểu thức N = \(\dfrac{\sqrt{x}+1}{\sqrt{\text{x}}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)
\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện
Đúng 3
Bình luận (2)
Tìm điều kiện xác định và rút gọn biểu thức:
B=\(\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{3}{x-9}\right):\dfrac{1}{\sqrt{x}-3}\)
ĐKXĐ: \(x\ge0;x\ne9\)
\(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{3}{x-9}\right):\dfrac{1}{\sqrt{x}-3}\)
\(=\left[\dfrac{\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right]:\dfrac{1}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}-3}{1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
Đúng 7
Bình luận (0)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >9\end{matrix}\right.\)
\(B=\dfrac{\sqrt{x}-3+3}{x-9}\cdot\left(\sqrt{x}-3\right)=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
Đúng 2
Bình luận (0)
cho biểu thức Q=(√x/√x-2+1/√x+2-2/4-√x):√2+3/√x-2 tìm điều kiện xác định và rút gọn Q
Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn. Viết ntn khó nhìn quá.
Đúng 0
Bình luận (0)

a) Tìm điều kiện xác định và rút gọn biểu thức P.
b) Với x thỏa mãn điều kiện xác định của P, chứng minh rằng P < 2.
a) \(P=\left(\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}-\frac{2}{4-x}\right):\frac{\sqrt{x}+3}{\sqrt{x}-2}\left(ĐK:x\ge0;x\ne4\right)\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}-2+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(=\frac{x+2\sqrt{x}+\sqrt{x}}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}=\frac{\sqrt{x}}{\sqrt{x}+2}\)
b) Vì: \(\sqrt{x}+4>0,\forall x\inĐK\)
=> \(2\sqrt{x}+4>\sqrt{x}\)
=> \(\frac{\sqrt{x}}{2\sqrt{x}+4}< 0\)
=> \(\frac{\sqrt{x}}{\sqrt{x}+2}< 2\)
=>đpcm
Đúng 0
Bình luận (0)