29.

Do \(M\in\Delta\) nên tọa độ có dạng: \(M\left(m;2m+1\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(m-4;2m+4\right)\\\overrightarrow{BM}=\left(m-5;2m-4\right)\\\overrightarrow{CM}=\left(m-1;2m+2\right)\end{matrix}\right.\)

\(\Rightarrow AM^2+BM^2+CM^2\)

\(=\left(m-4\right)^2+\left(2m+4\right)^2+\left(m-5\right)^2+\left(2m-4\right)^2+\left(m-1\right)^2+\left(2m+2\right)^2\)

\(=15m^2-12m+78\)

\(=15\left(m-\dfrac{2}{5}\right)^2+\dfrac{378}{5}\ge\dfrac{378}{5}\)

Dấu "=" xảy ra khi \(m=\dfrac{2}{5}\Rightarrow M\left(\dfrac{2}{5};\dfrac{9}{5}\right)\)

30.

Đặt \(f\left(x\right)=x^2-6x-7\)

Đồ thị hàm \(y=\left|f\left(x\right)\right|=\left|x^2-6x-7\right|\) được tạo ra bằng cách lấy đối xứng phần bên dưới trục Ox của đồ thị \(f\left(x\right)\) lên như hình vẽ:

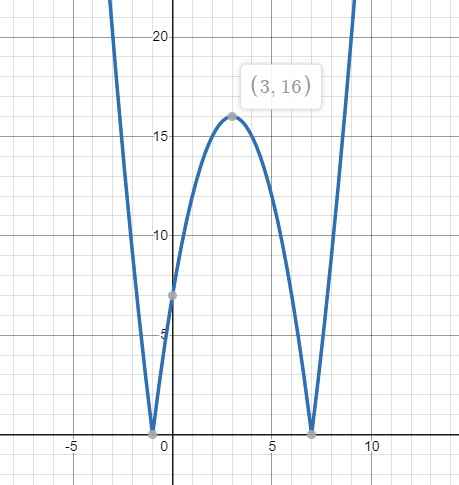
Từ đồ thị ta thấy pt có 4 nghiệm pb khi và chỉ khi: \(0< m< 16\)

\(\Rightarrow\) Có 15 giá trị nguyên của m

3.

\(\left|x-2\right|=2-x\Leftrightarrow\left|2-x\right|=2-x\)

\(\Leftrightarrow2-x\ge0\Rightarrow x\le2\) (quy tắc trị tuyệt đối: \(\left|A\right|=A\Leftrightarrow A\ge0\))

6. Đề bài sai (có lẽ do in nhầm)

Tập xác định của pt này là R

8.

Đặt \(\sqrt{x^2+3x+3}=t>0\Rightarrow x^2+3x+1=t^2-2\)

\(\Rightarrow t^2+t-2=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-2\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow x^2+3x+3=1\Rightarrow\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)

9.

\(\Leftrightarrow\left|\left(x+1\right)\left(x+4\right)\right|=x+4\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+4\ge0\\\left[{}\begin{matrix}x+4=0\\\left|x+1\right|=1\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge-5\\\left[{}\begin{matrix}x=-4\\x=0\\x=-2\end{matrix}\right.\end{matrix}\right.\) (3 nghiệm đều thỏa mãn)

Câu 23: A

Câu 24: C

Năm thường có 365 ngày (tháng 2 có 28 ngày), năm nhuận có 366 ngày (tháng 2 có 29 ngày). Kể từ 8 tháng 3 năm 2004 thì sau 60 năm sẽ là 8 tháng 3 năm 2064. Cứ 4 năm sẽ có 1 năm nhuận, năm 2064 cũng là năm nhuận.

Trong 60 năm này có số năm nhuận là 60: 4 +  1 = 16 năm. Nhưng vì qua tháng 2 của năm 2004 nên từ 8 tháng 3 năm 2004 đến 8 tháng 3 năm 2064 có 15 năm có 366 ngày và 45 năm có 365 ngày.

Vì thế 60 năm có số ngày là: 366 x 15 + 365 x 45 = 21915 (ngày)

Mỗi tuần lễ có 7 ngày nên ta có: 21915 : 7 = 3130 (tuần) dư 5 ngày.

Vì 8 tháng 3 năm 2004 là thứ 3 nên 8 tháng 3 năm 2064 là chủ nhât.

Năm thường có 365 ngày ﴾tháng 2 có 28 ngày﴿, năm nhuận có 366 ngày ﴾tháng 2 có 29 ngày﴿. Kể từ 8 tháng 3 năm 2004 thì sau 60 năm sẽ là 8 tháng 3 năm 2064. Cứ 4 năm sẽ có 1 năm nhuận, năm 2064 cũng là năm nhuận. Trong 60 năm này có số năm nhuận là 60: 4 + 1 = 16 năm. Nhưng vì qua tháng 2 của năm 2004 nên từ 8 tháng 3 năm 2004 đến 8 tháng 3 năm 2064 có 15 năm có 366 ngày và 45 năm có 365 ngày. Vì thế 60 năm có số ngày là: 366 x 15 + 365 x 45 = 21915 ﴾ngày﴿ Mỗi tuần lễ có 7 ngày nên ta có: 21915 : 7 = 3130 ﴾tuần﴿ dư 5 ngày. Vì 8 tháng 3 năm 2004 là thứ 3 nên 8 tháng 3 năm 2064 là chủ nhât. 

1B 2A(nhấn âm 1,còn lại nhấn âm 2) 3B 4A(Although->Despite) 5A 6C 7C 8B 9B 10D 11A 12C

13.In spite of the cold weather, our teacher wasn't wearing the coat

14.These machine has been sold by my brother for 2 days

\(4,=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{5-2\sqrt{6}-9}=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}\\ =\dfrac{3\left(3-\sqrt{2}-\sqrt{3}\right)}{2+\sqrt{6}}=\dfrac{\left(9-3\sqrt{2}-3\sqrt{3}\right)\left(\sqrt{6}-2\right)}{2}\\ =\dfrac{9\sqrt{6}-18-6\sqrt{3}+6\sqrt{2}-9\sqrt{2}+6\sqrt{3}}{2}\\ =\dfrac{9\sqrt{6}-3\sqrt{2}-18}{2}\)

\(7,=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-2-\sqrt{3}\\ =\sqrt{3}+2+\sqrt{2}+1-2-\sqrt{3}=1+\sqrt{2}\)

\(10,\dfrac{1}{\sqrt{a}+\sqrt{a+2}}=\dfrac{\sqrt{a}-\sqrt{a+2}}{a-a-2}=\dfrac{\sqrt{a-2}-\sqrt{a}}{2}\)

Do đó \(\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{5}}+...+\dfrac{1}{\sqrt{47}+\sqrt{49}}\)

\(=\dfrac{\sqrt{3}-\sqrt{1}+\sqrt{5}-\sqrt{3}+...+\sqrt{49}-\sqrt{47}}{2}=\dfrac{-1+\sqrt{49}}{2}=\dfrac{7-1}{2}=3\)

10, \(\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{5}}+...+\dfrac{1}{\sqrt{17}+\sqrt{19}}=\dfrac{\sqrt{1}-\sqrt{3}}{\left(\sqrt{1}+\sqrt{3}\right)\left(\sqrt{1}-\sqrt{3}\right)}+\dfrac{\sqrt{3}-\sqrt{5}}{\left(\sqrt{3}+\sqrt{5}\right)\left(\sqrt{3}-\sqrt{5}\right)}+...+\dfrac{\sqrt{17}-\sqrt{19}}{\left(\sqrt{17}+\sqrt{19}\right)\left(\sqrt{17}-\sqrt{19}\right)}=\dfrac{1-\sqrt{3}+\sqrt{3}-\sqrt{5}+...+\sqrt{17}-\sqrt{19}}{-2}=-\dfrac{1-\sqrt{19}}{2}\)