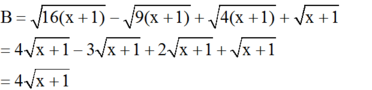a) Rút gọn:

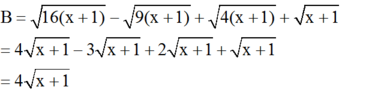
b) Để B = 16 thì:

⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)

Rút gọn:

a.

\(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\left(x\ge-1\right)\)

\(B=\sqrt{16}.\sqrt{x+1}-\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}+\sqrt{x+1}\)

\(B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)

\(B=\left(4-3+2+1\right).\sqrt{x+1}\)

\(B=4.\sqrt{x+1}\)

b.

\(B=16\\\)

\(\Rightarrow4\sqrt{x+1}=16\)

\(\Rightarrow\sqrt{x+1}=\dfrac{16}{4}=4\)

\(\Rightarrow x+1=4^2\)

\(\Rightarrow x+1=16\rightarrow x=16-1=15\) (thỏa mãn)

vậy x=15

a) Pt \(\Leftrightarrow\sqrt{\left(x-2\right)^2}=5\Leftrightarrow\left|x-2\right|=5\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)

Vậy...

b)Đk: \(x\ge-1\)

Pt \(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}=16-\sqrt{x+1}\)

\(\Leftrightarrow4\sqrt{x+1}=16\)\(\Leftrightarrow x+1=16\)\(\Leftrightarrow x=15\) (tm)

Vậy...

\(A=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\) (a>0)

\(=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)

\(=a+\sqrt{a}-\left(2\sqrt{a}+1\right)+1=a-\sqrt{a}\)

b) \(A=a-\sqrt{a}=a-2.\dfrac{1}{2}\sqrt{a}+\dfrac{1}{4}-\dfrac{1}{4}=\left(\sqrt{a}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

Dấu "=" xảy ra khi \(\sqrt{a}=\dfrac{1}{2}\Leftrightarrow a=\dfrac{1}{4}\left(tmđk\right)\) 

Vậy \(A_{min}=-\dfrac{1}{4}\)

a) \(\sqrt{x^2-4x+4}=5\Rightarrow\sqrt{\left(x-2\right)^2}=5\Rightarrow\left|x-2\right|=5\)

\(\Rightarrow\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=7\\x=-3\end{matrix}\right.\)

b) \(\sqrt{16x+16}-3\sqrt{x+1}+\sqrt{4x+4}=16-\sqrt{x+1}\)

\(\Rightarrow\sqrt{16\left(x+1\right)}-3\sqrt{x+1}+\sqrt{4\left(x+1\right)}+\sqrt{x+1}=16\)

\(\Rightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)

\(\Rightarrow4\sqrt{x+1}=16\Rightarrow\sqrt{x+1}=4\Rightarrow x=15\)

a) \(A=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\)

\(=\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}-\dfrac{\sqrt{a}\left(2\sqrt{a}+1\right)}{\sqrt{a}}+1\)

\(=a+\sqrt{a}-2\sqrt{a}-1+1=a-\sqrt{a}\)

b) Ta có: \(a-\sqrt{a}=\left(\sqrt{a}\right)^2-2.\sqrt{a}.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\dfrac{1}{4}\)

\(=\left(\sqrt{a}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)

\(\Rightarrow A_{min}=-\dfrac{1}{4}\) khi \(a=\dfrac{1}{4}\)

✱ giải pt:

a.\(\sqrt{x^2-4x+4}\)\(=5\)

⇔\(\sqrt{\left(x-2\right)^2}=5\)

⇒\(\left[{}\begin{matrix}x-2=5\\x-2=-5\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)

vậy....

b.\(\sqrt{16x+16}-3\sqrt{x+1}+\sqrt{4x+4}=16-\sqrt{x+1}\)

⇔ \(4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)

⇔ \(4\sqrt{x+1}=16\)

⇔ \(\sqrt{x+1}=16\)

⇒ \(x+1=256\)

⇔ \(x=255\)

vậy.....

\(a,A=\dfrac{4\left(x-4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{4}{x+4}\\ b,B=\dfrac{x+4+x+2x-4}{x\left(x+4\right)}=\dfrac{4x}{x\left(x+4\right)}=\dfrac{4}{x+4}=A\)

a) \(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\)

\(=\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}+\sqrt{4\left(x+1\right)}+\sqrt{x+1}\)

\(=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=4\sqrt{x+1}\)

b) \(B=4\sqrt{x+1}=16\) khi \(\sqrt{x+1}=4\) hay x+1=16 => x=15

a: \(B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)

\(=4\sqrt{x+1}\)

b: Để B=16 thì \(4\sqrt{x+1}=16\)

=>x+1=16

hay x=15