Cho hình bình hành ABCD có \(\widehat{A}=2\widehat{B}\) và AD=AB khi đó số đo \(\widehat{BAC}\)

Những câu hỏi liên quan
Bài 22: Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Chưng minh:1) Tư giác AMND là hình bình hành.2) Tư giác BMDN là hình bình hành.Bài 24: Cho hình bình hành ABCD có AB AD. Tia phân giác của widehat{A}căt BC tại I, tia phân giác của widehat{C}căt AD ở K.1) Chưng minh: Tam giác ABI là tam giác cân.2) So sánh widehat{BIA}và widehat{KCB}.3) Chưng minh: Tư giác AICK là hình bình hành.
Đọc tiếp
Bài 22: Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Chưng minh:
1) Tư giác AMND là hình bình hành.
2) Tư giác BMDN là hình bình hành.
Bài 24: Cho hình bình hành ABCD có AB < AD. Tia phân giác của \(\widehat{A}\)căt BC tại I, tia phân giác của \(\widehat{C}\)căt AD ở K.
1) Chưng minh: Tam giác ABI là tam giác cân.
2) So sánh \(\widehat{BIA}\)và \(\widehat{KCB}\).
3) Chưng minh: Tư giác AICK là hình bình hành.
Bài 22 :
Vì ABCD là hình bình hành
=> AB = DC
Mà M là trung điểm AB
=> AM = MB
Mà N là trung điểm DC
=> DN = NC
=> AM = DN
Mà AB//DC
=> DN//AM
=> AMND là hình bình hành
Chứng minh tương tự ta có : MBCN là hình bình hành
Đúng 0
Bình luận (0)
Cho hình thang ABCD có \(\widehat{A}\)=\(\widehat{B}\)=\(90^0\);AB= BC=\(\frac{1}{2}\)AD. Khi đó số đo của \(\widehat{ACD}\)là:
Xem chi tiết
Trong tam giác ABC có:
AB=BC=\(\frac{1}{2}\)AD ; nên tam giác ABC cân tại B
=>\(\widehat{BAC}\)=\(\widehat{BCA}\)(1)
mà \(\widehat{ABC}\)+\(\widehat{BAC}\)+\(\widehat{BCA}\)=\(^{180^0}\)
\(\widehat{BAC}\)+\(\widehat{BCA}\)=\(^{180^0}\)-\(^{90^0}\)
\(\widehat{BAC}\)+\(\widehat{BCA}\)=\(^{90^0}\)(2)
Từ (1) và (2) suy ra:
\(\widehat{BAC}\) =\(\widehat{BCA}\) =\(^{ }45^0\)
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD) có \(\widehat{B}-\widehat{C}=60\) độ và \(\widehat{D}=\dfrac{4}{5}\widehat{A}\).
Tính số đo các góc của hình thang ABCD
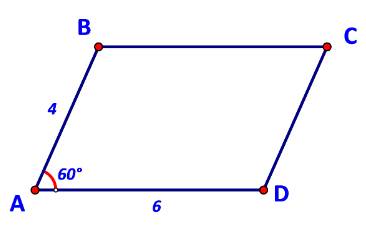
Cho hình bình hành ABCD có AB = 4, AD = 6, \(\widehat {BAD} = {60^o}\) (Hình 73).
a) Biểu thị các vecto \(\overrightarrow {BD} ,\overrightarrow {AC} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} .\)
b) Tính các tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AD} ,\;\overrightarrow {AB} .\overrightarrow {AC} ,\;\overrightarrow {BD} .\overrightarrow {AC} .\)
c) Tính độ dài các đường chéo \(BD,AC.\)
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)
Đúng 0
Bình luận (0)
cho hình thang ABCD (AD//BC,AD>BC) có đường chéo AC vuông góc với cạnh bên CD,\(\widehat{BAC}=\widehat{CAD}\) và \(\widehat{D}=60^0\)
a)chứng minh ABCD là hình thang cân
b)tính độ dài đáy AD,biết chu vi hình thang bằng 20cm
Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân \(ABCD\) (hình 4). Cho biết \(\widehat D = \widehat C = 75^\circ \). Tìm số đo \(\widehat A\) và \(\widehat B\).

Do ${ABCD}$ là hình thang cân (gt) nên \(\widehat A = \widehat B\)
Xét hình thang \(ABCD\) ta có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} + \widehat {\rm{D}} = 360^\circ \)
\(\begin{array}{l}\widehat A + \widehat B + 75^\circ + 75^\circ = 360^\circ \\\widehat A + \widehat B = 210^\circ \end{array}\)
Mà \(\widehat A = \widehat B\) (cmt)
Suy ra : \(\widehat {\rm{A}} = \widehat B = 105^\circ \)
Đúng 0
Bình luận (0)
Bài 1 : Hình thoi ABCD có góc B = 120 và AB = 5 cm . Khi đó độ dài đoạn BD là :
Bài 2 : Cho hình thang ABCD có cạnh = 2 cm , góc A = 60 . Khi đó độ dài đường chéo AC của hình thang là :
Bài 3 : Cho hình bình hành ABCD có góc A = 2 . góc B và AD = AB . Khi đó số đo của góc BAC là
Bai 1:
Ta co: BD la duong cheo vua la duong phan giac ( T/c cua duong cheo trong hinh thoi )
Thay co goc B = 120 cm, suy ra goc ABC = 60 do
Tam giac ABC la tam giac deu
AB = AD = BD = 5
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^o\) ; \(\widehat{CAD}=90^o\).
Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB và IJ.
Cho tứ diện ABCD, có \(\widehat{BAC}=90^0,\widehat{CAD}=60^0,\widehat{BAD}=120^0;AB=AC=AD=a\). Tính khoảng cách từ B đến (ACD).
A. \(\dfrac{a\sqrt{6}}{3}\)
B. \(\dfrac{a\sqrt{3}}{2}\)
C. \(\dfrac{a\sqrt{6}}{2}\)
D. \(\dfrac{a\sqrt{3}}{4}\)





















