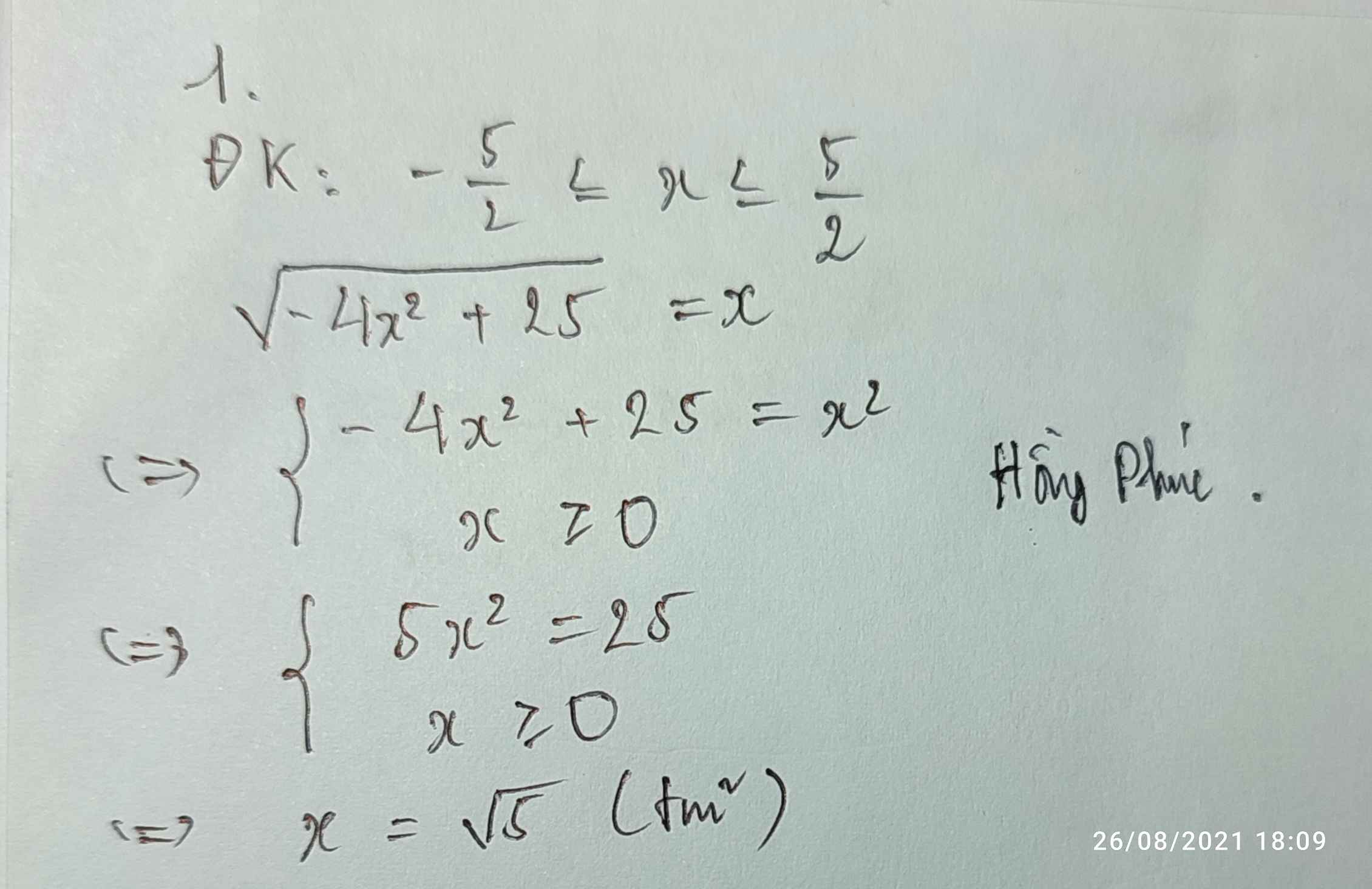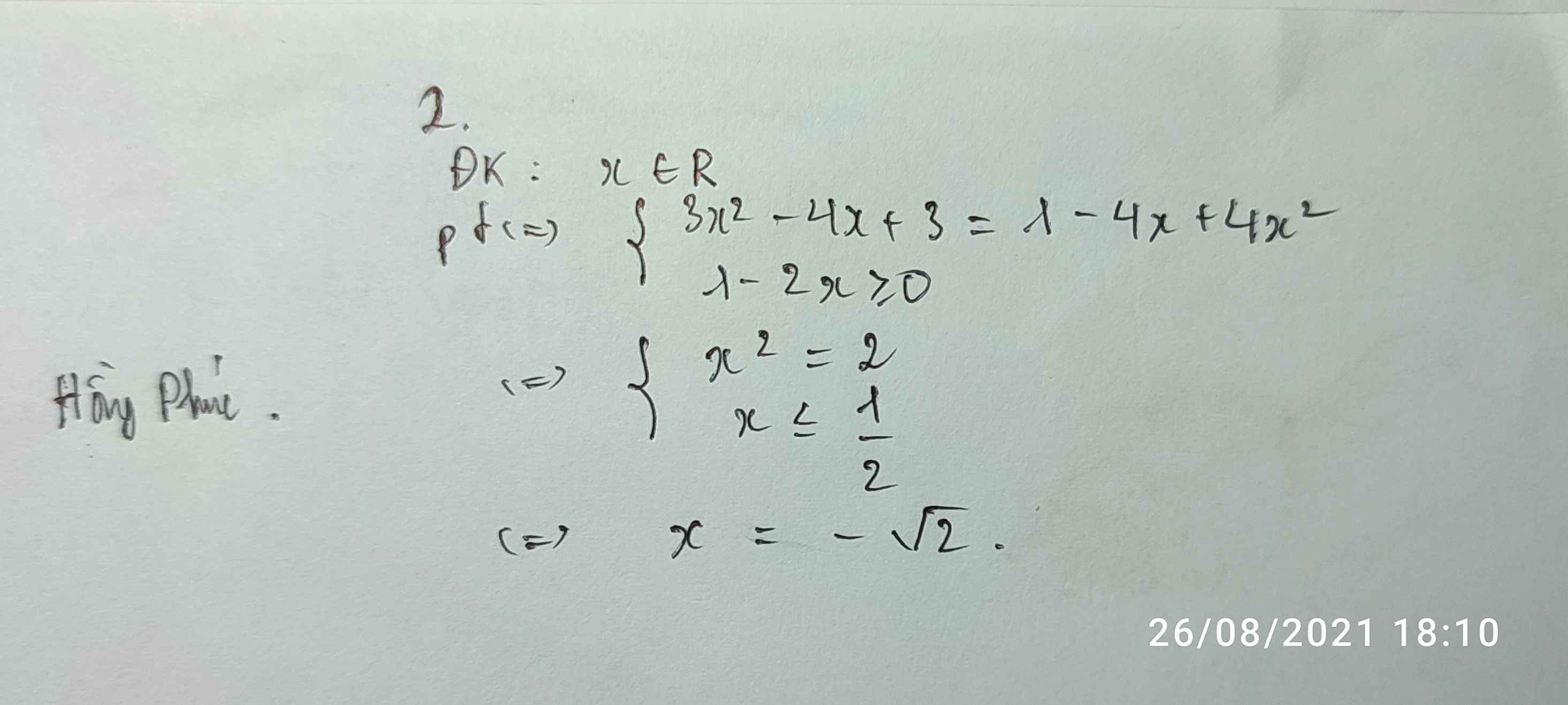a

ĐK:

 \(3-x\ge0\\ \Leftrightarrow x\le3\)

\(\sqrt{x^2-3x+2}=3-x\\ \Leftrightarrow x^2-3x+2=\left(3-x\right)^2=9-6x+x^2\\ \Leftrightarrow x^2-3x+2-9+6x-x^2=0\\ \Leftrightarrow3x=7\\ \Leftrightarrow x=\dfrac{7}{3}\left(nhận\right)\)

Thử lại: \(\sqrt{\left(\dfrac{7}{3}\right)^2-3.\dfrac{7}{3}+2}=\dfrac{2}{3}>0\)

Vậy phương trình có nghiệm duy nhất \(x=\dfrac{7}{3}\)

b

\(\sqrt{4x^2-20x+25}=\sqrt{\left(2x\right)^2-2.2x.5+5^2}=\sqrt{\left(2x-5\right)^2}=\left|2x-5\right|\)

Phương trình trở thành:

\(\left|2x-5\right|+2x=5\) (1)

Với \(x< \dfrac{5}{2}\) thì (1) \(\Leftrightarrow5-2x+2x=5\Leftrightarrow5=5\) 

=> Với \(x< \dfrac{5}{2}\) thì phương trình có nghiệm với mọi x \(< \dfrac{5}{2}\) (I)

Với \(x\ge\dfrac{5}{2}\) thì (1)

 \(\Leftrightarrow2x-5+2x=5\\ \Leftrightarrow2x-5+2x-5=0\\ \Leftrightarrow4x=10\\ \Leftrightarrow x=\dfrac{10}{4}=\dfrac{5}{2}\left(nhận\right)\left(II\right)\)

Từ (I), (II) kết luận phương trình có nghiệm với mọi \(x\le\dfrac{5}{2}\)

c

\(\Leftrightarrow\left|3-2x\right|=4\) (1)

Nếu \(x\le\dfrac{3}{2}\) thì (1)

\(\Leftrightarrow3-2x=4\\ \Leftrightarrow2x=-1\\ \Leftrightarrow x=-\dfrac{1}{2}\left(nhận\right)\)

Nếu \(x>\dfrac{3}{2}\) thì (1)

\(\Leftrightarrow2x-3=4\\ \Leftrightarrow2x=7\\ \Leftrightarrow x=\dfrac{7}{2}\left(nhận\right)\)

Vậy phương trình có 2 nghiệm \(S=\left\{-\dfrac{1}{2};\dfrac{7}{2}\right\}\)

a: =>x^2-3x+2=x^2-6x+9 và x<=3

=>3x=7 và x<=3

=>x=7/3(loại)

b: =>|2x-5|=5-2x

=>2x-5<=0

=>x<=5/2

c: =>|2x-3|=4

=>2x-3=4 hoặc 2x-3=-4

=>x=-1/2 hoặc x=7/2

a: =>|2x-1|=3

=>2x-1=3 hoặc 2x-1=-3

=>2x=-2 hoặc 2x=4

=>x=2 hoặc x=-1

c: \(\Leftrightarrow\left|x-3\right|=11-x\)

=>x<=11 và (x-3)^2=(11-x)^2

=>x<=11 và x^2-6x+9=x^2-22x+121

=>x<=11 và 16x=112

=>x=7

d:

ĐKXĐ: 3x+19>=0

=>x>=-19/3

PT =>x>=-3 và (3x+19)=(x+3)^2=x^2+6x+9

=>x>=-3 và x^2+6x+9-3x-19=0 

=>x>=-3 và (x+5)(x-2)=0

=>x=2

e: =>\(\sqrt{x^2+x+5}=x+1\)

=>x>=-1 và x^2+x+5=x^2+2x+1

=>x>=-1 và 2x+1=x+5

=>x=4

\(2M=\left(\sqrt{x^2-3x+25}-\sqrt{x^2-3x+9}\right)\)\(\left(\sqrt{x^2-3x+25}+\sqrt{x^2-3x+9}\right)\)

\(2M=x^2-3x+25-x^2+3x-9=16\)

M = 8

1:

\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-2\right)=0\)

=>x-3=0 hoặc \(\sqrt{x+3}=2\)

=>x=3 hoặc x+3=4

=>x=1(loại) hoặc x=3(nhận)

2:

\(\Leftrightarrow\left(\sqrt{4x+1}-\sqrt{3x-4}\right)^2=1\)

=>\(4x-1+3x-4-2\sqrt{\left(4x+1\right)\left(3x-4\right)}=1\)

=>\(\sqrt{4\left(4x+1\right)\left(3x-4\right)}=7x-6\)

=>4(12x^2-16x+3x-4)=(7x-6)^2

=>49x^2-84x+36=48x^2-52x-16

=>-84x+36=-52x-16

=>-32x=-52

=>x=13/8

3: =>\(\sqrt{\left(x-5\right)^2}=5-x\)

=>|x-5|=5-x

=>x-5<=0

=>x<=5

4: \(\Leftrightarrow\left|x-4\right|=x+2\)

=>\(\left\{{}\begin{matrix}x>=-2\\\left(x-4\right)^2=\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-2\\x^2-8x+16=x^2+4x+4\end{matrix}\right.\)

=>x>=-2 và -8x+16=4x+4

=>x=1

tthTrần Thanh PhươngNguyễn Việt LâmAkai HarumaLê Thị Thục HiềnNguyễn Thị Ngọc ThơNguyễn Huy ThắngFa Châu De

Bạn lưu ý lần sau viết đẩy đủ đề bài.

Yêu cầu đề bài mình đoán là rút gọn

\(\frac{\sqrt{x}+2}{\sqrt{x}+3}-\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{x\sqrt{x}+3x-25}{x+\sqrt{x}-6}=\frac{(\sqrt{x}+2)(\sqrt{x}-2)-(\sqrt{x}+3)^2}{(\sqrt{x}+3)(\sqrt{x}-2)}+\frac{x\sqrt{x}+3x-25}{(\sqrt{x}+3)(\sqrt{x}-2)}\)

\(=\frac{x-4-(x+6\sqrt{x}+9)+x\sqrt{x}+3x-25}{(\sqrt{x}+3)(\sqrt{x}-2)}=\frac{x\sqrt{x}+3x-6\sqrt{x}-38}{(\sqrt{x}+3)(\sqrt{x}-2)}\)

Rút gọn ra kết quả hơi xấu. Có lẽ phân thức thứ 2 bạn nên đổi lại thành $\frac{\sqrt{x}-3}{\sqrt{x}-2}$