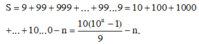\(99^{2n}=\left(99^2\right)^n=\left(...01\right)^n=\left(...01\right)\)

\(99^{2n+1}=99^{2n}.99=\left(...01\right).99=\left(...99\right)\)

\(99^{99}=\left(99^2\right)^{49}.99=\left(...01\right).99=\left(...99\right)\)

(100⁹⁹+99⁹⁹)¹⁰⁰=100^99x100+99^99x100

(100¹⁰⁰+99¹⁰⁰)⁹⁹=100^100x99+99^100x99

Vì100^100x99+99^100x99=100^99x100+99^99x100

=>M=N

Các bạn nhớ nha !!!

các cậu kết bạn với mình nha

Mk ko hiểu lắm!Sao (100⁹⁹+99⁹⁹)¹⁰⁰=100^99x100+99^{99x100 dc?}

Đáp án đúng : B

\(M=\frac{99}{1}+\frac{98}{2}+\frac{97}{3}+...+\frac{2}{98}+\frac{1}{99}\)

cộng vào mỗi phân số trong 98 phân số sau,trừ phân số cuối đi 98 , ta được :

\(M=1+\left(\frac{98}{2}+1\right)+\left(\frac{97}{3}+1\right)+...+\left(\frac{2}{98}+1\right)+\left(\frac{1}{99}+1\right)\)

\(M=\frac{100}{100}+\frac{100}{2}+\frac{100}{3}+...+\frac{100}{98}+\frac{100}{99}\)

chuyển phân số \(\frac{100}{100}\)ra sau , ta được :

\(M=\frac{100}{2}+\frac{100}{3}+...+\frac{100}{98}+\frac{100}{99}+\frac{100}{100}\)

\(M=100.\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{98}+\frac{1}{99}+\frac{1}{100}\right)\)

\(\Rightarrow\frac{M}{N}=\frac{100.\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{98}+\frac{1}{99}+\frac{1}{100}\right)}{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}+\frac{1}{100}}=100\)

Thank bn na !!!

Lớp 6 dữ chc 🙄

câu này là của lớp mấy đó

Tính can N là gì thế?

Can N là gì có hỏi can đâu