Tính AB biết AC=4cm,BC=5cm

Những câu hỏi liên quan
Cho tam giác ABC vuông tại a a tính AC biết BC=13cm AB=5cm b tính BC biết AB=4cm AC=7cm
a, Áp dụng định lý Pitago:
`AB^2 + AC^2 = BC^2`
`=> 25 + AC^2 = 169`
`=> AC^2 = 144`
`=> sqrt 144 = 12`.
b. Áp dụng định lý Pytago ta có:
`AB^2 + AC^2 = BC^2`
`16 + 49 = BC^2`
`BC^2 = 65`
`BC = sqrt 65`.
Đúng 5
Bình luận (0)
Áp dụng định lí Pitago trong tam giác ABC vuông tại A
AC = BC2 + AB2
= 132 + 52
= \(\sqrt{194}\) = 14 cm
Áp dụng định lí Pitago trong tam giác ABC cân tại A
BC = AB2 + AC2
= 42 + 72
= \(\sqrt{65}\) = 8 cm
Đúng 1
Bình luận (0)
1.
a) Cho ΔABC có : AC=5cm, BC=3cm. Tìm cạnh AB biết, AB là số nguyên và AB>6cm
b) Cho ΔABC có: AB=8cm, AC=6cm. Tính BC, biết BC là số nguyên BC<4cm
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
Đúng 1
Bình luận (0)
Tính các góc của tam giác ABC, biết AB = 3cm, AC = 4cm và BC = 5cm
Ta có: AB = 3 ⇒ A B 2 = 3 2 = 9
AC = 4 ⇒ A C 2 = 4 2 = 16
BC = 5 ⇒ B C 2 = 5 2 = 25
Ta có: A B 2 + A C 2 = 9 + 16 = 25 = B C 2
Suy ra tam giác ABC vuông tại A.
Ta có:
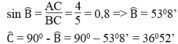
Đúng 0
Bình luận (0)
Cho tam giác ABC. Đường thẳng a// BC cắt AC, AB tại M, N .a) Biết AM =4cm, AN = 5cm, AC =8,5. Tính MBb) Biết NB= 10,5cm, AN =9cm, AC= 8,5. Tính AMc) Biết AM = 9,5, MB= 28, MN= 8. Tính BC
b) Ta có: AN+NB=AB(N nằm giữa A và B)
nên AB=9+10,5=19,5(cm)
Xét ΔABC có
N\(\in\)AB(gt)
M\(\in\)AC(gt)
MN//BC(gt)
Do đó: \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{9}{19.5}=\dfrac{AM}{8.5}\)
\(\Leftrightarrow AM=\dfrac{9\cdot8.5}{19.5}=\dfrac{51}{13}cm\)
Vậy: \(AM=\dfrac{51}{13}cm\)
Đúng 2
Bình luận (0)
Cho hình vẽ bên (Hình 2)
Biết AB = 4cm, AC = 6cm, BC = 5cm
phân giác AD và BE||AC
Tính độ dài BD, BE
Theo tính chất tia phân giác và tính chất dãy tỉ số bằng nhau ta có:
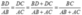
Từ BE//AC nên chứng minh được DABE cân tại B Þ BE = 4cm
Đúng 0
Bình luận (0)
cho hình trong đó AE vuông BC . tính AB biết AE =4cm,AC=5cm , Bc=9cm
Cho tam giác ABC , vẽ AH vuông góc với BC tại H (H thuộc BC ) biết AC =5cm , BC =9cm , AH =4cm . Tính độ dài AB .
Hình vẽ:
Xét \(\Delta ACH\left(\widehat{H}=90^0\right)\)có:
\(AC^2=AH^2+HC^2\)( định lý py-ta-go )
\(\Rightarrow5^2=4^2+HC^2\)
\(\Rightarrow HC^2=5^2-4^2\)
\(\Rightarrow HC^2=25-16\)
\(\Rightarrow HC^2=9\)
\(\Rightarrow HC=\sqrt{9}\)
\(\Rightarrow HC=3cm\)
Ta có: \(BH+HC=9cm\)
mà \(HC=3cm\left(cmt\right)\)
\(\Rightarrow BH=9-3=6cm\)
Xét \(\Delta AHB\left(\widehat{H}=90^0\right)\)có:
\(AB^2=AH^2+BH^2\)( định lý py-ta-go )
\(\Rightarrow AB^2=4^2+6^2\)
\(\Rightarrow AB^2=16+36\)
\(\Rightarrow AB^2=52\)
\(\Rightarrow AB=\sqrt{52}cm\)
Vậy độ dài cạnh AB là \(\sqrt{52}cm\)
Cho ΔABC có AB =4cm , AC = 5cm , A = 60 ° . Tính BC
Kẻ BH vuông góc với AC tại H.
Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta được:
\(BH=sinA\cdot AB=sin60^0.4=2\sqrt{3}\left(cm\right)\)
\(AH=cosA.AB=cos60^0.4=2\left(cm\right)\)
Suy ra BH = 3(cm).
Áp dụng định lý Py-ta-go vào tam giác BHC vuông tại H, ta được:
\(BC=\sqrt{BH^2+CH^2}=\sqrt{12+9}=\sqrt{21}\left(cm\right)\)
Vậy BC = \(\sqrt{21}\)(cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC có đường cao AH. Biết AC=5cm, HC=4cm. Tính AB, CH, AH và BC.
Áp dụng định lý py-ta-go vào tam giác AHC vuông tại H có :
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AH^2=AC^2-HC^2\)
\(\Leftrightarrow AH=\sqrt{5^2-4^2}=3\left(cm\right)\)
Áp dung hệ thức lượng vào tam giá ABC vuông tại A , ta có :
+) \(AH^2=BH.HC\)
\(\Leftrightarrow9=BH.4\)
\(\Leftrightarrow BH=\frac{9}{4}\left(cm\right)\)
+) \(AB^2=AH.BH\)
\(\Leftrightarrow AB^2=\left(4+\frac{9}{4}\right).\frac{9}{4}=\frac{225}{16}\left(cm\right)\)
+) \(BC=4+\frac{9}{4}=\frac{25}{4}\left(cm\right)\)



















