Tìm m để phương trình x4 - 2x2 + m = 0 có 4 nghiệm phân biệt

Những câu hỏi liên quan
Tìm m để phương trình
x
4
-
2
x
2
+
3
–
m
2
+
2
m
0
có đúng ba nghiệm phân biệt A. m -1 B. m 3 C. -1 m 3 D. Cả A và B
Đọc tiếp
Tìm m để phương trình x 4 - 2 x 2 + 3 – m 2 + 2 m = 0 có đúng ba nghiệm phân biệt
A. m = -1
B. m = 3
C. -1 < m < 3
D. Cả A và B
Chọn D
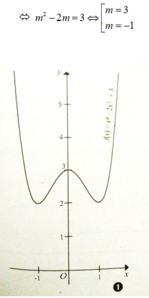
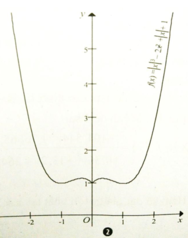
Xét hàm số y = x 4 - 2 x 2 + 3 ( C )
Đồ thị có dạng như hình (1)
x 4 - 2 x 2 + 3 - m 2 + 2 m = 0 có đúng ba nghiệm phân biệt <=> Đường thẳng y = m 2 + 2 m cắt đồ thị C tại ba điểm phân biệt
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để phương trình
x
4
−
2
x
2
−
m
0
có bốn nghiệm phân biệt. A.
−
2
m
0
B.
0
m
1
C.
−
1
m
2
D.
−
1
m...
Đọc tiếp
Tìm tất cả các giá trị của m để phương trình x 4 − 2 x 2 − m = 0 có bốn nghiệm phân biệt.
A. − 2 < m < 0
B. 0 < m < 1
C. − 1 < m < 2
D. − 1 < m < 0
Đáp án D
Đặt t = x 2 ⇒ t ≥ 0. Phương trình đã cho trở thành t 2 − 2 t − m = 0 *
Để phương trình đã cho có 4 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt
⇔ Δ ' = 1 + m > 0 S = 2 > 0 P = − m > 0 ⇔ − 1 < m < 0
Đúng 0
Bình luận (0)
Tìm m để phương trình
x
4
-
2
x
2
-
m
3
có 2 nghiệm phân biệt A.
m
-
3
,
m
-
4
B.
m
≤
-
4
C.
m
≥
-
3
,
m
4
D.
m
≥
-
3
Đọc tiếp
Tìm m để phương trình x 4 - 2 x 2 - m = 3 có 2 nghiệm phân biệt
A. m > - 3 , m = - 4
B. m ≤ - 4
C. m ≥ - 3 , m = 4
D. m ≥ - 3
Đáp án A
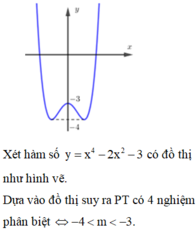
Xét hàm y = x 4 – 2 x 2 – 3
Ta có: y’ = 4x3 – 4x
⇒ y’ = 0 ⇔ x = 0 hoặc x = -1 hoặc x = 1
Ta có bảng biến thiên
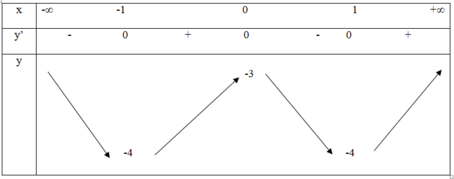
Số phương trình có 2 nghiệm phân biệt
bằng số giao điểm giữa đồ thị hàm số y = x 4 – 2 x 2 – 3 và đường thẳng y = m
ð ⇒ m = -4 hoặc m > -3
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình x 4 − 2 x 2 − 3 = m có 4 nghiệm phân biệt.
A. -1 < m < 1
B. m < -4
C. -4 < m < -3
D. m > -1
Cho hàm số
y
x
4
-
2
x
2
-
3
có đồ thị như hình bên. Tìm tất cả các giá trị của tham số m để phương trình
x
4
-
2
x
2
-
3
2
m
-
4
có hai nghiệm phân biệt. A.
m
∈
(
-
∞...
Đọc tiếp
Cho hàm số y = x 4 - 2 x 2 - 3 có đồ thị như hình bên. Tìm tất cả các giá trị của tham số m để phương trình x 4 - 2 x 2 - 3 = 2 m - 4 có hai nghiệm phân biệt.
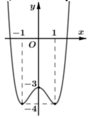
A. m ∈ ( - ∞ ; 1 2 ]
B. m ∈ - ∞ ; 0 ∪ 1 2
C. m ∈ 0 ; 1 2
D. m ∈ 0 ∪ 1 2 ; + ∞
Từ đồ thị hàm số, suy ra phương trình x 4 - 2 x 2 - 3 = 2 m - 4 có hai nghiệm phân biệt khi và chỉ khi
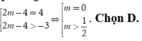
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để phương trình: x 4 + 2 x 2 + 1 = m có hai nghiệm phân biệt.
A. m ≥ 1
B. m > 1
C. m < 1
D. m < 0
Đáp án B
Đồ thị hàm số y = x 4 + 2 x 2 + 1 có dạng
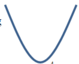
Với điểm cực tiểu là (0;1) nên để phương trình x 4 + 2 x 2 + 1 = m có hai nghiệm thì m>1 .
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
|
x
4
-
2
x
2
|
m
có 3 nghiệm thực phân biệt A. 0m1 B. m0 C. m1 D. m1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình | x 4 - 2 x 2 | = m có 3 nghiệm thực phân biệt
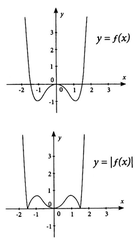
A. 0<m<1
B. m=0
C. m=1
D. m>1
Cho hàm số
y
-
x
4
+
2
x
2
có đồ thị như hình vẽ bên Tìm tất cả các giá trị thực của tham số m để phương trình
-
x
4
+
2
x
2
log
2
m
có bốn nghiệm thực phâ...
Đọc tiếp
Cho hàm số y = - x 4 + 2 x 2 có đồ thị như hình vẽ bên
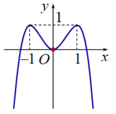
Tìm tất cả các giá trị thực của tham số m để phương trình - x 4 + 2 x 2 = log 2 m có bốn nghiệm thực phân biệt.
![]()
![]()
![]()
![]()
Cho phương trình x4 - 2( m+1 )x2 + 2m+1 = 0
Tìm m để phương trình có 4 nghiệm phân biệt
Đặt \(x^2=t\left(t\ge0\right)\), phương trình trở thành:
\(t^2-2\left(m+1\right)t+2m+1=0\left(1\right)\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(1\right)\) có hai nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2>0\\t_1+t_2=2m+2>0\\t_1t_2=2m+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m\ne0\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho phương trình: x 4 - 13 x 2 + m = 0 . Tìm các giá trị của m để phương trình: Có 4 nghiệm phân biệt

Phương trình (1) có 4 nghiệm phân biệt khi phương trình (2) có hai nghiệm số dương khi
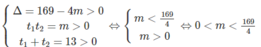
Đúng 0
Bình luận (0)