a/ x^3-3x^2-4x+12
b/ x^4-5x^2+4
c/(x+y+z)^3-x^3-y^3-z^3 Phân tích đa thức thành nhân tử
Phân tích các đa thức sau thành nhân tử:
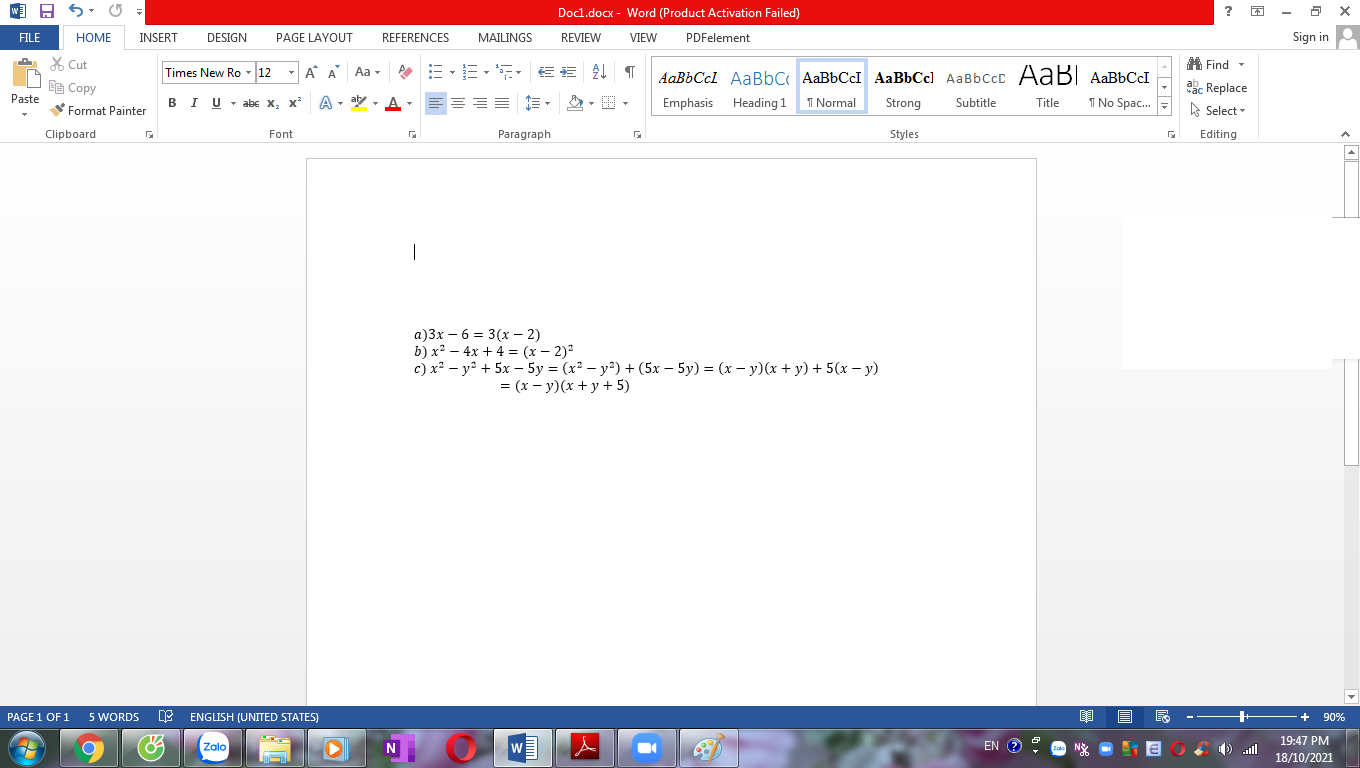
a) 3x-6
b) x2-4x+4
c) x2-y2+5x-5y
d) 8(x+y+z)3-(x+y)3-(y+z)3-(y+z)3-(z+x)3
Do câu d mình ko biết làm bởi v mình không làm được
1.Đa thức 4x(2y-z) +7y(2y-z) được phân tích thành nhân tử là :
A .(2y+z)(4x+7y)
B.(2y-z)(4x-7y)
C.(2y+z)(4x-7y)
D. (2y-z)(4x+7y)
2 Phân tích đa thức x2+3x+xy+3y thành nhân tử ta được :
A. (x+3)(y+3)
B. (x-y)(x+3)
C. (x+3)(x+y)
D. Cả 3 đều sai
Đa thức x^3 - 2x^2 + x - xy^2 được phân tích thành nhân tử
Đa thức x^3 + 3x^2y +3xy^2 + y^3 được phân tích thành nhân tử là
Đa thức 4x(2y-z)+7y(2y-z) được phân tích thành nhân tử là:
Đa thức x^2+4x+4 được phân tích thành nhân tử là
Tìm x biết x(x-2)-x+2
\(1,=x\left(x^2-2x+1-y^2\right)=x\left[\left(x-1\right)^2-y^2\right]=x\left(x-y-1\right)\left(x+y-1\right)\\ 2,=\left(x+y\right)^3\\ 3,=\left(2y-z\right)\left(4x+7y\right)\\ 4,=\left(x+2\right)^2\\ 5,Sửa:x\left(x-2\right)-x+2=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Phân tích các đa thức sau thành nhân tử:
a)x^3-3x^2-ã+12
b)x^4-5x^2+4
c)(x+y+z)^3-x^3-y^3-z^3
Phân tích các đa thức sau thành nhân tử :
a) \(x^3-3x^2-4x+12\)
b) \(x^4-5x^2+4\)
c) \(\left(x+y+z\right)^3-x^3-y^3-z^3\)
a) x^3−3x^2−4x+12
=(x^3-3x^2)-(4x-12)
=x^2(x-3)-4(x-3)
=(x-3)(x^2-4)=(x-3)(x-2)(x+2)
b) x^4-5x^2+4=x^4-x^2-4x^2+4
=(x^4-x^2) - ( 4x^2-4)
=x^2(x^2-1) - 4(x^2-1)
=(x^2-1)(x^2-4)
=(x-1)(x+1)(x-2)(x+2)
c) (x+y+z)^3-x^3-y^3-z^3
=x^3+y^3+z^3+3x^2yz+3xy^2z+3xyz^2-x^3-y^3-z^3
=3x^2yz+3xy^2z+3xyz^2
3xyz(x+y+z)
Phân tích đa thức thành nhân tử:
(x-y)3 + (y-z)3 + (z-x)3
x2y2(y-x)+y2z2(z-y)-z2x2(z-x)
x8+x4+1
9a3-13a+6
Phân tích đa thức thành nhân tử bằng phương pháp đồng nhất hệ số:
x4-3x3+6x2-5x+3
a) \([(x-y)3 + (y-z)3]+ (z-x)3\)=\(\left(x-y+y-z\right)\left[\left(x-y\right)^2-\left(x-y\right)\left(y-z\right)+\left(y-z\right)^2\right]-\left(x-z\right)^3\)
\(=\left(x-z\right)\left[\left(\left(x-y\right)^2-\left(x-y\right)\left(y-z\right)+\left(y-z\right)^2-\left(x-z\right)^2\right)\right]\)
\(=\left(x-z\right)\left[\left(x-y\right)\left(x-y-y+z\right)+\left(y-z-x+z\right)\left(y-z+x-z\right)\right]=\left(x-z\right)\left[\left(x-2y+z\right)\left(x+z\right)-\left(x-y\right)\left(x+y-2z\right)\right]\)
\(=\left(x-z\right)\left(x-y\right)\left(x-2y+z-x-y+2z\right)=\left(x-z\right)\left(x-y\right)\left(z-y\right)3\)
b) \(=y^2\left(x^2y-x^3+z^3-z^2y\right)-z^2x^2\left(z-x\right)=y^2\left[-y\left(z^2-x^2\right)-\left(z^3-x^3\right)\right]-z^2x^2\left(z-x\right)\)
\(=y^2\left(z-x\right)\left(-yz-xy-z^2-zx-x^2\right)-z^2x^2\left(z-x\right)=\left(z-x\right)\left(-y^3z-xy^2-z^2y^2-xyz-x^2y^2-z^2x^2\right)\)
đến đây coi như là thành nhân tử rồi nha. em muốn gọn thì ráng ngồi nghĩ rồi tách nha. chỉ cần nhóm mấy cái có ngoặc giống nhau là đc. k khó đâu. chịu khó nghĩ để rèn luyện nha
c) \(x^8+2x^4+1-x^4=\left(x^4+1\right)^2-x^4=\left(x^4+1-x^2\right)\left(x^4+1+x^2\right)\)
\(\left(9a^3-6a^2\right)+\left(6a^2-4a\right)+\left(-9a+6\right)=3a^2\left(3a-2\right)+2a\left(3a-2\right)-3\left(3a-2\right)=\left(3a-2\right)\left(3a^2+2a-3\right)\)
d) em sửa đề đi. đề sai rồi. đồng nhất hệ số phải có dấu bằng nha.
có gì liên hệ chị. đúng nha ;)
Phân tích đa thức thành nhân tử
1. (x^2+y^2+z^2).(x+y+z)^2+(xy+yz+xz)^2
2. (x+1)^4 +(x^4+x^2+1)
3. 4x^4+4x^3+5x^2+2x+1
Phân tích đa thức sau thành nhân tử:
a,x^6+3x^5+4x^4+4x^3+4x^2+3x+1
b,x^10+x^5+1
c,(x+y+z)^3-x^3-y^3-z^3
ai lm đúng mk tick cho
x^10 + x^5 + 1
= x^10 + x^9 - x^9 + x^8 - x^8 + x^7 - x^7 + x^6 - x^6 + x^5 + x^5 - x^5 + x^4 - x^4 + x^3 - x^3 + x^2 - x^2 + x - x + 1
= (x^10 + x^9 + x^8) - (x^9 + x^8 + x^7) + (x^7 + x^6 + x^5) - (x^6 + x^5 + x^4) + (x^5 + x^4 + x^3) - (x^3 + x^2 + x) + (x^2 + x + 1)
= x^8 (x^2 + x + 1) - x^7 (x^2 + x + 1) + x^5 (x^2 + x + 1) - x^4 (x^2 + x + 1) + x^3 (x^2 + x + 1) - x (x^2 + x + 1) + (x^2 + x + 1)
= (x^2 + x + 1) (x^8 - x^7 + x^5 - x^4 + x^3 - x + 1)
x^6 + 3x^5 + 4x^4 + 4x^3 + 4x^2 + 3x + 1
Câu này có thể áp dụng định lý : nếu tổng các hệ số biến bậc chắn và tổng các hệ số biến bậc lẻ bằng nhau thì đa thức có nhân tử x + 1
- Nhận thấy : 1+4+4+1 = 3+4+3
x^6 + 3x^5 + 4x^4 + 4x^3 + 4x^2 + 3x + 1
= ( x^6 + x^5 ) + ( 2x^5 + 2x^4 ) + ( 2x^4 + 2x^3 ) + ( 2x^3 + 2x^2 ) + ( 2x^2 + 2x ) + ( x+ 1 )
= x^5.(x+1) + 2x^4.(x+1) + 2x^3.(x+1) + 2x^2.(x+1) + 2x.(x+1) + ( x+1 )
= ( x+1 )( x^5 + 2x^4 + 2x^3 + 2x^2 + 2x + 1 )
Tiếp tục phân tích bằng cách trên vì 1+2+2 = 2+2+1
= ( x+1)(x+1)(x^4 + x^3 + x^2 + x +1 )
= (x+1)^2 . ( x^4 + x^3 + x^2 + x + 1 )
phân tích các đa thức sau thành nhân tử:
a, x3 -3x2 -4x+12
b, x4 -5x2 +4
c, (x+y+z)3 -x3 -y3 -z3
a)\(x^3-3x^2-4x+12\)
\(=\left(x^3-3x^2\right)-\left(4x-12\right)\)
\(=\left(x-3\right)\left(x^2-4\right)\)
\(=\left(x-2\right)\left(x+2\right)\left(x-3\right)\)
b) \(x^4-5x^2+4\)
\(=\left(x^4-4x^2\right)-\left(x^2-4\right)\)
\(=\left(x^2-4\right)\left(x^2-1\right)\)
\(=\left(x+1\right)\left(x-1\right)\left(x+2\right)\left(x-2\right)\)
c) \(\left(x+y+z\right)^3-x^3-y^3-z^3\)
\(=\left(x+y\right)^3+3\left(x+y\right)\left(x+y+z\right)z+z^3-x^3-y^3-z^3\)
\(=x^3+y^3+3xy\left(x+y\right)+3\left(x+y\right)\left(xz+yz+z^2\right)-x^3-y^3\)
\(=3\left(x+y\right)\left(xy+yz+zx+z^2\right)\)
\(=3\left(x+y\right)\left(y+z\right)\left(z+x\right)\)