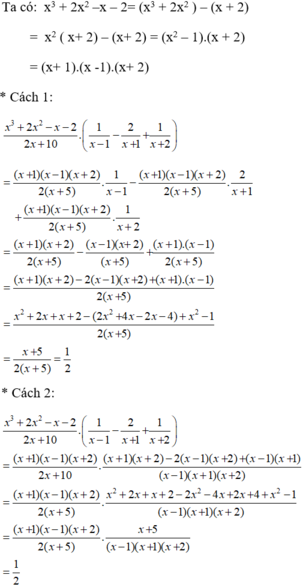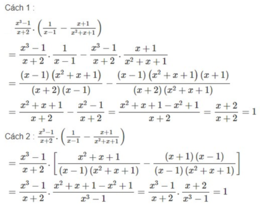Hãy dùng tính chất phân phối để thực hiện phép nhân x.(2x+3)

Những câu hỏi liên quan
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này:
x
3
+
2
x
2
-
x
-
2
2
x
+
10
.
1
x...
Đọc tiếp
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này: x 3 + 2 x 2 - x - 2 2 x + 10 . 1 x - 1 - 2 x + 1 + 1 x + 2
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này:
x
3
-
1
x
+
2
.
1
x
-
1
-...
Đọc tiếp
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này: x 3 - 1 x + 2 . 1 x - 1 - x + 1 x 2 + x + 1
Thực hiện các phép tính sau bằng hai cách : dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này :
a) \(\dfrac{x^3-1}{x+2}.\left(\dfrac{1}{x-1}-\dfrac{x+1}{x^2+x+1}\right)\)
b) \(\dfrac{x^3+2x^2-x-2}{2x+10}\left(\dfrac{1}{x-1}-\dfrac{2}{x+1}+\dfrac{1}{x+2}\right)\)
a: \(=\dfrac{x^3-1}{x+2}\cdot\dfrac{x^2+x+1-x^2+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\left(\dfrac{x+1-2x+2}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\left(\dfrac{-\left(x-3\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x+2}\right)\)
\(=\dfrac{\left(x+2\right)\left(x-1\right)\left(x+1\right)}{2\left(x+5\right)}\cdot\dfrac{-\left(x^2-x-6\right)+x^2-1}{\left(x-1\right)\left(x+1\right)\left(x+2\right)}\)
\(=\dfrac{-x^2+x+6+x^2-1}{2\left(x+5\right)}=\dfrac{x+5}{2\left(x+5\right)}=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Cho biểu thức M = \(\frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\). Hãy tính giá trị của M theo 2 cách:
a) Thực hiện tính nhân rồi cộng 2 kết quả
b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng
a)
\(\begin{array}{l}M = \frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\\ = \frac{{ - 5}}{{56}} + \frac{{ - 11}}{{56}} = \frac{{ - 16}}{{56}} = \frac{{ - 2}}{7}\end{array}\)
b)
\(\begin{array}{l}M = \frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\\ = \frac{1}{7}.[(\frac{{ - 5}}{8}) + (\frac{{ - 11}}{8})]\\ = \frac{1}{7}.\frac{{ - 16}}{8}\\ = \frac{1}{7}.( - 2)\\ = \frac{{ - 2}}{7}\end{array}\)
Đúng 0
Bình luận (0)
Dùng tính chất phân phối của phép cộng và phép nhân để tính nhanh
5{ - 3 + 2 } - 7 { 5 - 4 }
-3 [ 4 - 7 ] + 5{ -3 + 2 }
Sử dụng tính chất phân phối phép nhân đối phép cộng rồi thực hiện phép tính sau:
a) -78x31-78x24-78x17+22x72
Ta có : -78 x 31 - 78 x 24 - 78 x 17 + 22 x 72
= 78 x (-31 - 24 - 17) + 22 x 72
= -78 x 72 + 22 x 72
= 72 x (-78 + 22)
= 72 x -56
= -4032
-78 x 31 - 78 x 24 - 78 x 17 + 22 x 72
=78 x(-31 - 24 -17)+22x72
=-78 x 72+22 x 72
=72 x (-78+22)
=-4200
Có thể tính nhẩm tích 45.6 bằng cách: Áp dụng tính chất kết hợp của phép nhân: 45.6 45.(2.3) (45.2).3 90 .3 270 Áp dụng tính chất phân phối của phép nhân đối với phép cộng: 45.6 (40+ 5).6 40.6 + 5.6 240 +30 270 Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng: 25.12; 34.11; 47.101
Đọc tiếp
Có thể tính nhẩm tích 45.6 bằng cách:
Áp dụng tính chất kết hợp của phép nhân:
45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270
Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270
Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng:
25.12; 34.11; 47.101
Áp dụng tính chất phân phối của phép nhân đối với phép cộng: a(b+c)=ab+ac ta có:
25.12 = 25.(10 + 2) = 25.10 + 25.2 = 250 + 50 = 300.
34.11 = 34.(10 + 1) = 34.10 + 34 = 340 + 34 = 374.
47.101 = 47.(100 + 1) = 47.100 + 47.1 = 4700 + 47 = 4747.
Đúng 0
Bình luận (0)
Áp dụng tính chất phân phối của phép nhân đối với phép cộng, hãy tìm tích 2x.(3x2 – 8x + 1) bằng cách nhân 2x với từng hạng tử của đa thức 3x2 – 8x +1 rồi cộng các tích tìm được
Đa thức 3x2 – 8x +1 có các hạng tử là: 3x2 ; -8x ; 1
Ta có: 2x . 3x2 = (2.3). (x.x2) = 6x3
2x. (-8x) = [2.(-8) ]. (x.x) = -16x2
2x. 1 = 2x
Vậy 2x.(3x2 – 8x + 1) = 6x3 -16x2 + 2x
Đúng 1
Bình luận (0)
Dùng tính chất phân phối của phép nhân với phép cộng để tính : a, 157.17 - 157 . 7 b, 5. ( -3 +2 ) - 7. ( 5-4) c, 17. ( -84) + 17. ( -16) d, -145 . ( 13 - 57 ) + 57 . ( 10- 145 ) e, 199. ( 15-17) - 199. ( -17 + 5)
\(a,157.17-157.7=157\left(17-7\right)=1570\)
\(b,5.\left(-3+2\right)-7.\left(5-4\right)=-5-7=-12\)
\(c,17.\left(-84\right)+17\left(-16\right)=17\left[\left(-84\right)+\left(-16\right)\right]=-1700\)
\(d,-145.\left(13-57\right)+57.\left(10-145\right)=6380-7695=-1315\)
\(e,199.\left(15-17\right)-199.\left(-17+5\right)=199.10=1990\)
Đúng 1
Bình luận (0)