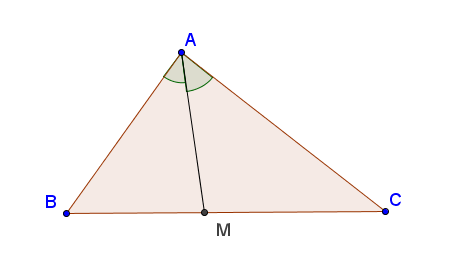
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.

Những câu hỏi liên quan
Chứng minh rằng trọng tâm của một tam giác cách đều 3 đỉnh của tam giác đó
Bạn biết rằng đường trung tuyến của tam giác đều cũng là đường phân giác của tam giác
Mà <A = <B = <C ( dấu góc đó nhe bạn, mình k bik bấm dấu góc ở đâu hết :) )
=> <A / 2 = <B / 2 = <C / 2
=> <A1 = <A2 = <B1 = <B2 = <C1 = <C2
Xét tam giác AHC có: <A1 = <C1 => tam giác AHC là tam giác cân tại H => AH = HC (1)
Xét tam giác HCB có: <C1 = <B2 => tam giác BHC là tam giác cân tại H => HC = HB (2)
Xét tam giác BHA có: <B2 = <A2 => tam giác BHA là tam giác cân tại H => HB = HA (3)
Từ (1), (2), (3) => HA = HB = HC => điều phải chứng minh
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi G là trọng tâm tam giác. H là trực tâm tam giác. I là giao điểm 3 đường phân giác. O là điểm cách đều 3 đỉnh tam giác.
Chứng minh rằng: tam giác ABC là tam giác đều khi và chỉ khi các điểm G,H,I,O trùng nhau và ngược lại.
Thiên Ngoại Phi Tiên sai rồi cậu lấy trêm mạn mà đúng gì nẫu nói G là trực tâm H là đường cao , o cách đều ba đỉnh mà sao không có ba diểm đó
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng trong tam giác đều, điểm cách đều 3 cạnh của tam giác là trọng tâm của tam giác đó.

Vì \(\Delta ABC\) đều nên AB = AC = BC (tính chất tam giác đều)
Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC
Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của \(\Delta ABC\)
Tương tự, ta cũng được BI, CI là đường trung tuyến của \(\Delta ABC\)
Vậy I là giao điểm của ba đường đường trung tuyến của \(\Delta ABC\) nên I là trọng tâm của \(\Delta ABC\).
Chú ý:
Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.
Đúng 0
Bình luận (0)
Cho tam giác ABC, H là trực tâm, G là trọng tâm, O là điểm cách đều 3 đỉnh của tam giác ABC. Chứng minh H,G,O thẳng hàng và HG= 2GO
chứng minh rằng trong một tam giác cân ABC ( AB=AC ) , đỉnh A . Trọng tâm G và điểm I nằm trong tam giác cách đều ba cạnh là ba điểm cùng nằm trên một đường thẳng
.1.Cho tam giác ABC cân tại A có AD là đường phân giác. a) Chứng minh tam giác ABD tam giác ACDb) Gọi G là trọng tâm tam giác ABC. Chứng minh ba điểm A, G, D thẳng hàng.c) Tính DG biết AB 13cm,BC 10cm2.Cho tam giác ABC vuông ở A, có AB 16cm,AC 30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.3.Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt C ở N. Biết AN MN, BN cắt AM ở O. Chứng minh: a) Tam giác ABC cân ở Ab) O là trọng tâm t...
Đọc tiếp
.1.Cho tam giác ABC cân tại A có AD là đường phân giác.
a) Chứng minh tam giác ABD = tam giác ACD
b) Gọi G là trọng tâm tam giác ABC. Chứng minh ba điểm A, G, D thẳng hàng.
c) Tính DG biết AB 13cm,BC 10cm
2.Cho tam giác ABC vuông ở A, có AB = 16cm,AC = 30cm. Tính tổng các khoảng cách từ trọng tâm G của tam giác đến các đỉnh của tam giác.
3.Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt C ở N. Biết AN = MN, BN cắt AM ở O. Chứng minh: a) Tam giác ABC cân ở A
b) O là trọng tâm tam giác ABC.
4.Cho tam giác cân ABC, trung tuyến AM. Đường trung trực của AB cắt AM ở O. Chứng minh rằng điểm O cách đều 3 đỉnh của tam giác ABC.
Cần gấp ạ!
Gọi cho là ai trọng tâm của tam giác đều ABC cạnh 2 cm chứng minh cách đều ba cạnh của tam giác ABC từ đó tính khoảng cách từ G tới mỗi canh của 1 tam giác
chứng minh trong tam giác ABC,nếu trực tâm O cách đều 3 đỉnh thì tam giác ABC đều
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
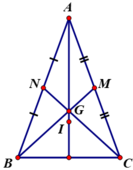
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà 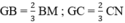 (Tính chất trọng tâm của tam giác)
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
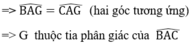
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của 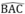
Vì G, I cùng thuộc tia phân giác của 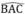 nên A, G, I thẳng hàng
nên A, G, I thẳng hàng
Đúng 0
Bình luận (0)