Trong Hình 8 dưới đây, hãy chọn ra các cặp hình đồng dạng với nhau.

Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.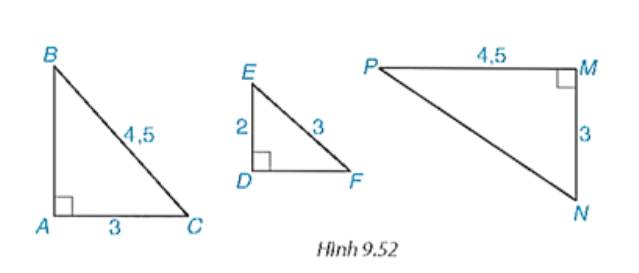
Ta có:
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)
Cho hình bên là tam giác ABC vuông tại A, đường cao AH. Trong hình bên có bao nhiêu cặp tam giác đồng dạng với nhau. Hãy chỉ ra các cặp đồng dạng và theo các đỉnh tương ứng.
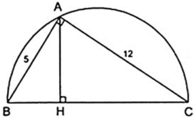
Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.
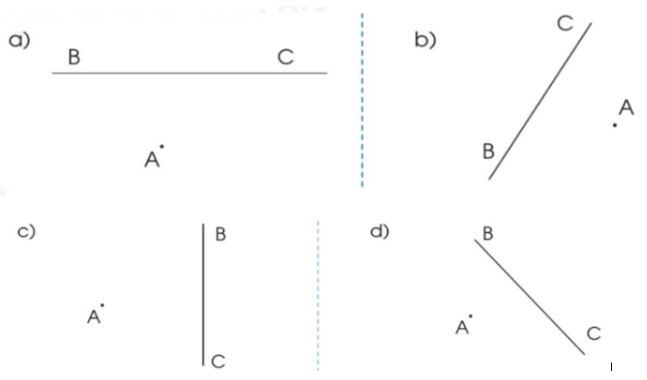
Hãy chỉ ra các cặp đường thẳng song song với nhau trong mỗi hình dưới đây.
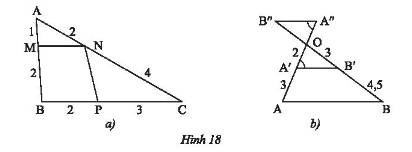
a) \(AB = AM + MB = 1 + 2 = 3;AC = AN + NC = 2 + 4 = 6;BC = BP + PC = 2 + 3 = 5\)
Ta có: \(\frac{{AM}}{{AB}} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{2}{6} = \frac{1}{3}\).
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{3}\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(MN//BC\).
Ta có: \(\frac{{CN}}{{CA}} = \frac{4}{6} = \frac{2}{3};\frac{{CP}}{{CB}} = \frac{3}{5}\).
Vì \(\frac{{CN}}{{AC}} \ne \frac{{CP}}{{BC}}\left( {\frac{2}{3} \ne \frac{3}{5}} \right)\) nên theo định lí Thales đảo trong tam giác \(ABC\), ta có \(NP\) không song song với \(BC\).
b) Vì \(\widehat {B''A''O} = \widehat {OA'B'}\) mà hai góc này ở vị trí so le trong nên \(A''B''//A'B'\).
\(OA = OA' + A'A = 2 + 3 = 5;OB = OB' + B'B = 3 + 4,5 = 7,5\)
Ta có: \(\frac{{OA'}}{{OA}} = \frac{2}{5};\frac{{OB'}}{{OB}} = \frac{3}{{7,5}} = \frac{2}{5}\).
Vì \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}} = \frac{2}{5}\) nên theo định lí Thales đảo trong tam giác \(OAB\), ta có \(A'B'//AB\).
Vì \(\left\{ \begin{array}{l}A'B'//AB\\A'B'//A''B''\end{array} \right. \Rightarrow AB//A''B''\).
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
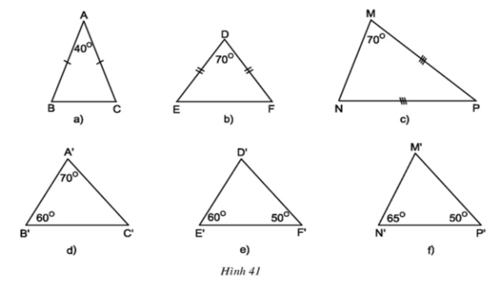
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)
Trong các tam giác dưới đây, những cặp tam giác nào đồng dạng với nhau ? Hãy giải thích (h.41)
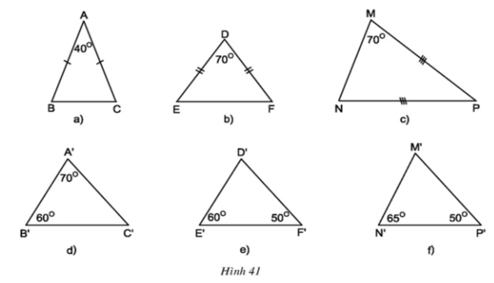
- ΔABC có ∠A + ∠B + ∠C = 180o ⇒ ∠B + ∠C = 180o - ∠A
Mà ΔABC cân tại A ⇒ ∠B = ∠C
⇒∠B = ∠C = ( 180o- 40o)/2 = 70o
ΔMNP cân tại P ⇒ ∠M = ∠N = 70o
ΔABC và ΔPMN có
∠B = ∠M = 70o)
∠C = ∠N = 70o)
⇒ ΔABC ∼ ΔPMN (g.g)
- ΔA’B’C’ có ∠A' + ∠B' + ∠C' = 180o
⇒∠C' = 180o- ( ∠A' + ∠B') = 180o - ( 70o+ 60o ) = 50o
ΔA’B’C’ và ΔD’E’F’ có
∠B' = ∠E' (= 60o)
∠C' = ∠F' (= 50o)
⇒ ΔA’B’C’ ∼ ΔD’E’F’ (g.g)
Chỉ ra các cặp đường thẳng song song với nhau, các cặp đường thẳng vuông góc với nhau trong hình dưới đây:
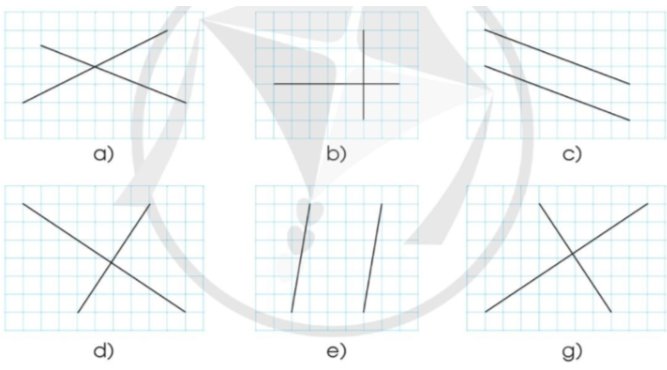
Các hình có các cặp đường thẳng song song với nhau: c, e
Các hình có các cặp đường thẳng vuông góc với nhau: b, d, g
Chỉ ra các cặp đường thẳng song song với nhau, các cặp đường thẳng vuông góc với nhau trong hình dưới đây:
Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.
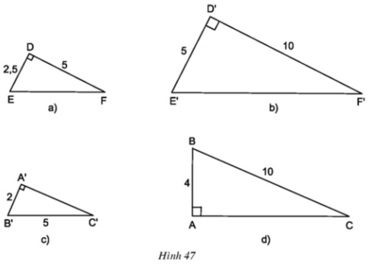
+ΔDEF vuông tại D và ΔD'E'F' vuông tại D’ có:
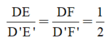
⇒ ΔDEF ∼ ΔD'E'F' (hai cạnh góc vuông)
*)Áp dụng định lí py ta go vào tam giác A’B’C’ vuông tại A’ có:
A’C’2 + A’B’2 = B’C’2
=> A’C’2 + 22 = 52
Suy ra: A’C’2 = 25 – 4 = 21 nên 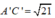
*)Áp dụng định lí py ta go vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
Thay số: 42 + AC2 = 102
Suy ra: AC2 = 100 – 16 = 84 nên

Do đó, ∆ A’B’C’ đồng dạng với tam giác ABC ( trường hợp 2).
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
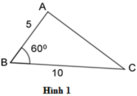
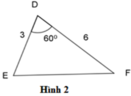
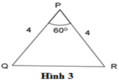
A. Hình 1 và hình 2
B. Hình 2 và hình 3
C. Hình 1 và hình 3
D. Tất cả đều đúng
Có:
B A B C = 5 10 = 1 2 ; D E D F = 3 6 = 1 2 ; P Q P R = 4 4 = 1 ⇒ B A B C = D E D F = 1 2
Xét ΔABC và ΔEDF ta có:
B A B C = D E D F (cmt) ⇔ D E B A = D F B C
B = D = 60 ∘ (gt)
=> ΔABC ~ ΔEDF (c - g - c).
Đáp án: A
Hãy chỉ ra các cặp tam giác đồng dạng với nhau từ các tam giác sau đây (h.38):
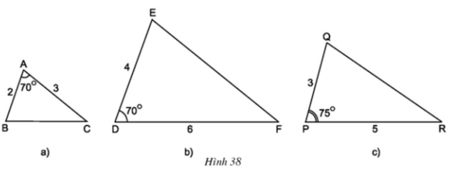
ΔABC và ΔDEF có
∠A = ∠D = 70o
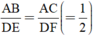
⇒ ΔABC ∼ ΔDEF (c.g.c)