Cho Hình 86.
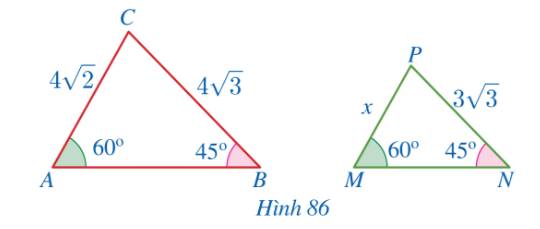
a) Chứng minh \(\Delta MNP \backsim \Delta ABC\)
b) Tìm \(x\).
Cho \(\Delta ABC \backsim \Delta MNP\).
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh \(\Delta ABD \backsim \Delta MNQ\).
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh \(\Delta ABG \backsim \Delta MNK\).
a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)
Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)
Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)
Xét tam giác ABD và tam giác MNQ có:
\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)
\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)
b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)
Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).
Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)
Xét tam giác ABG và tam giác NMK có:
\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)
\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)
Cho ΔABC \(\backsim\) ΔMNP, khẳng định nào sau đây không đúng?
a) ΔMNP \(\backsim\) ΔABC
b) ΔBCA \(\backsim\) ΔNPM
c) ΔCAB \(\backsim\) ΔPNM
d) ΔACB \(\backsim\) ΔMNP
Khẳng định d) là khẳng định không đúng
=> ΔACB \(\backsim\) ΔMPN
Cho hai tam giác ABC và MNP thỏa mãn \(\widehat A = 50^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat N = 60^\circ ,\,\,\widehat P = 70^\circ \). Chứng minh \(\Delta ABC \backsim \Delta MNP\).
Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 50^\circ + 60^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 70^\circ \end{array}\)
Xét tam giác ABC và tam giác MNP có:
\(\begin{array}{l}\widehat B = \widehat N = 60^\circ \\\widehat C = \widehat P = 70^\circ \end{array}\)
\( \Rightarrow \Delta ABC \backsim \Delta MNP\) (g-g).
Trong Hình 14, cho biết \(AB//CD\)
a) Chứng minh rằng \(\Delta AEB\backsim\Delta DEC\).
b) Tìm \(x\).
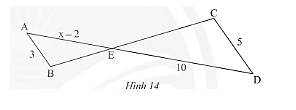
a) Xét tam giác \(ABE\) có:
\(AB//CD\) và \(C,D\) cắt \(BE;AE\) lần lượt tại \(C,D\).
Do đó, \(\Delta AEB\backsim\Delta DEC\) (định lí)
b) Vì \(\Delta AEB\backsim\Delta DEC\) nên \(\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số ta được:
\(\frac{{x - 2}}{{10}} = \frac{3}{5} \Rightarrow x - 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8\)
Vậy \(x = 8\).
Nếu \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) thì \(\Delta MNP\backsim\Delta ABC\) theo tỉ số
A. \(\frac{1}{3}\).
B. \(\frac{1}{9}\).
C. \(3\).
D. \(9\).
Đáp án đúng là A
Vì \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) nên \(\Delta MNP\backsim\Delta ABC\) theo tỉ số \(\frac{1}{3}\).
Trong Hình 19, cho biết \(MN//BC,MB//AC\)
a) Chứng minh rằng \(\Delta BNM\backsim\Delta ABC\)
b) Tính \(\widehat C\)
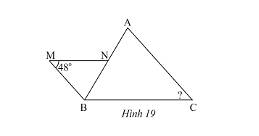
a) Vì \(MN//BC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)
Vì \(MB//AC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)
Xét tam giác \(BNM\) tam giác \(ABC\) ta có:
\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)
\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)
Do đó, \(\Delta BNM\backsim\Delta ABC\) (g.g)
b) Vì \(\Delta BNM\backsim\Delta ABC\) nên \(\widehat M = \widehat C = 48^\circ \) (hai góc tương ứng).
Quan sát Hình 12.
a) Chứng minh \(\Delta ABC\backsim\Delta A'B'C'\).
b) Tính độ dài cạnh \(B'C'\).
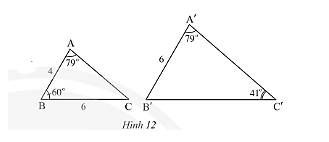
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).
Trong Hình 7, biết \(\Delta MNP\backsim\Delta ABC\) với tỉ số đồng dạng \(k = \frac{{MN}}{{AB}}\), hai đường cao tương ứng là \(MK\) và \(AH\).
a) Chứng minh rằng \(\Delta MNK\backsim\Delta ABH\)và \(\frac{{MK}}{{AH}} = k\).
b) Gọi \({S_1}\) là diện tích tam giác \(MNP\) và \({S_2}\) là diện tích tam giác \(ABC\). Chứng minh rằng \(\frac{{{S_1}}}{{{S_2}}} = {k^2}\).
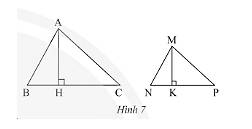
a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)
Cho \(\Delta ABC \backsim \Delta MNP\). Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì tam giác MNP cân tại đỉnh M.
b) Nếu tam giác ABC đều thì tam giác MNP đều.
c) Nếu \(AB \ge AC \ge BC\) thì \(MN \ge MP \ge NP\)
a) Tam giác ABC tại A nên \(\widehat B = \widehat C\) (1)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (2)
Từ (1) và (2) nên \(\widehat N = \widehat P\) suy ra tam giác MNP cân tại M.
b) Vì tam giác ABC là tam giác đều nên \(\widehat A = \widehat B = \widehat C = {60^o}\)(3)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (4)
Từ (3) và (4) suy ra \(\widehat M = \widehat N = \widehat P = {60^o}\) nên tam giác MNP là tam giác đều.
c) Vì tam giác ABC có \(AB \ge AC \ge BC\) suy ra \(\widehat C \ge \widehat B \ge \widehat A\) (quan hệ giữa góc và cạnh đối điện) (5)
Mà \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (6)
Từ (5) và (6) suy ra \(\widehat P \ge \widehat N \ge \widehat M\) nên \(MN \ge MP \ge NP\)