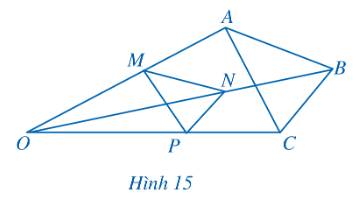
Trong Hình 15, cho \(MN\parallel AB,\,\,NP\parallel BC\). Chứng minh \(MP\parallel AC\).
Với giả thiết ở Bài tập 2, hãy:
a) Chứng minh rằng \(MN\parallel BC\). Tính khoảng cách giữa hai đường thẳng \(MN\) và \(BC\).
b) Chứng minh rằng \(MP\parallel \left( {BCD} \right)\). Tính khoảng cách từ đường thẳng \(MP\) đến mặt phẳng \(\left( {BCD} \right)\).
c) Chứng minh rằng \(\left( {MNP} \right)\parallel \left( {BCD} \right)\). Tính khoảng cách giữa hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {BCD} \right)\).
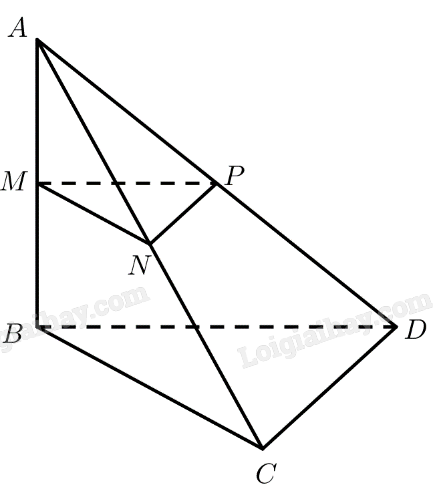
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(AC\)
\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MN\parallel BC\)
\(AB \bot BC \Rightarrow MB \bot BC \Rightarrow d\left( {MN,BC} \right) = MB = \frac{1}{2}AB = \frac{a}{2}\)
b) \(M\) là trung điểm của \(AB\)
\(P\) là trung điểm của \(A{\rm{D}}\)
\( \Rightarrow MP\) là đường trung bình của tam giác \(ABD\)
\(\left. \begin{array}{l} \Rightarrow MP\parallel BD\\B{\rm{D}} \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow MP\parallel \left( {BC{\rm{D}}} \right)\)
\(AB \bot \left( {BCD} \right) \Rightarrow MB \bot \left( {BCD} \right) \Rightarrow d\left( {MP,\left( {BCD} \right)} \right) = d\left( {M,\left( {BCD} \right)} \right) = MB = \frac{a}{2}\)
c)
\(\left. \begin{array}{l}\left. \begin{array}{l} \Rightarrow MN\parallel BC\\B{\rm{C}} \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {BC{\rm{D}}} \right)\\MP\parallel \left( {BC{\rm{D}}} \right)\\MN,MP \subset \left( {MNP} \right)\end{array} \right\} \Rightarrow \left( {MNP} \right)\parallel \left( {BC{\rm{D}}} \right)\)
\( \Rightarrow d\left( {\left( {MNP} \right),\left( {BCD} \right)} \right) = d\left( {M,\left( {BCD} \right)} \right) = MB = \frac{a}{2}\)
Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho \(MN\parallel BC\). Gọi I, P, Q lần lượt là giao điểm của BN và CM, AI và MN, AI và BC. Chứng minh:
a) \(\frac{{MP}}{{BQ}} = \frac{{PN}}{{QC}} = \frac{{AP}}{{AQ}}\)
b) \(\frac{{MP}}{{QC}} = \frac{{PN}}{{BQ}} = \frac{{IP}}{{IQ}}\)
a) Vì \(MP\parallel BQ\) nên ta có \(\frac{{MP}}{{BQ}} = \frac{{AP}}{{AQ}}\) (Định lý Thales)
Vì \(PN\parallel QC\) nên ta có \(\frac{{PN}}{{QC}} = \frac{{AP}}{{AQ}}\) (Định lý Thales)
\( \Rightarrow \frac{{MP}}{{BQ}} = \frac{{PN}}{{QC}} = \frac{{AP}}{{AQ}}\)
b) Vì \(MP\parallel QC\) nên \(\frac{{MP}}{{QC}} = \frac{{IP}}{{IQ}}\) (Hệ quả của định lý Thales)
Vì \(PN\parallel BQ\) nên \(\frac{{PN}}{{BQ}} = \frac{{IP}}{{IQ}}\) (Hệ quả của định lý Thales)
\( \Rightarrow \frac{{MP}}{{QC}} = \frac{{PN}}{{BQ}} = \frac{{IP}}{{IQ}}\)
Cho hình chóp \(S.ABC\) có \(SA = a\), góc giữa \(SA\) và \(mp\left( {ABC} \right)\) là \({60^ \circ }\). Gọi \(M,N\) lần lượt là trung điểm của cạnh \(SA\) và \(SB\). Chứng minh \(MN\parallel \left( {ABC} \right)\) và tính \(d\left( {MN,\left( {ABC} \right)} \right)\).
Kẻ \(SH\perp\left(ABC\right)\) \(\Rightarrow\widehat{SAH}=60^0\)
Áp dụng hệ thức lượng vào tam giác vuông có:
\(tan60^0=\dfrac{SH}{SA}\Leftrightarrow SH=\sqrt{3}a\)
Ta có M và N lần lượt là trung điểm của SA và SB
\(\Rightarrow\) MN là đường trung bình của tam giác ABC
\(\Rightarrow MN//BC\)
mà \(BC\subset\left(ABC\right)\) , \(MN⊄(ABC) \)
\(\Rightarrow MN//\left(ABC\right)\)
\(d\left(MN,\left(ABC\right)\right)=d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)=\dfrac{\sqrt{3}}{2}.a\)
Vậy \(d\left(MN,\left(ABC\right)\right)=\dfrac{\sqrt{3}}{2}a\)
Chứng minh \(d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)\)
Kẻ \(MK\perp\left(ABC\right)\Rightarrow MK//SH\)
Áp dụng định lý thales: \(\dfrac{MK}{SH}=\dfrac{AM}{AS}=\dfrac{1}{2}\)
\(\Rightarrow MK=\dfrac{1}{2}SH\Rightarrow d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)\) (đpcm)
Trong Hình 4, chứng tỏ rằng nếu \(MN\parallel BC\) thì \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\).
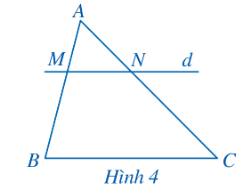
Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).
Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M,N,P,Q\) lần lượt là trung điểm của các cạnh \(AC,AA',A'C',BC\). Ta có:
A. \(\left( {MNP} \right)\parallel \left( {BCA} \right)\).
B. \(\left( {MNQ} \right)\parallel \left( {A'B'C'} \right)\).
C. \(\left( {NQP} \right)\parallel \left( {CAB} \right)\).
D. \(\left( {MPQ} \right)\parallel \left( {ABA'} \right)\).
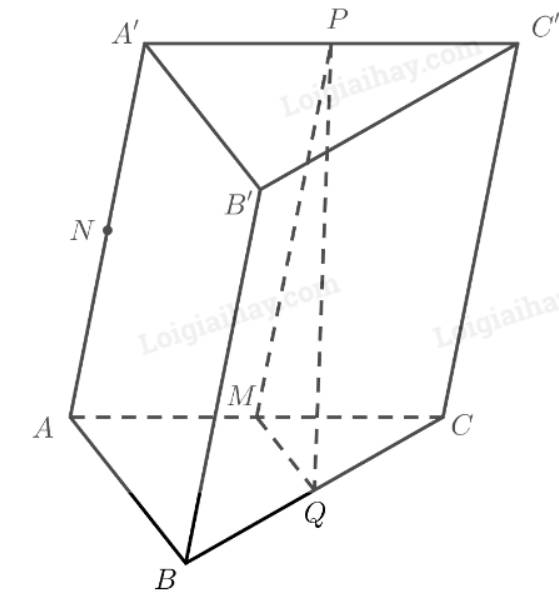
Ta có: \(M\) là trung điểm của \(AC\)
\(Q\) là trung điểm của \(BC\)
\( \Rightarrow MQ\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow MQ\parallel AB\\AB \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABA'} \right)\)
\(M\) là trung điểm của \(AC\)
\(P\) là trung điểm của \(A'C'\)
\( \Rightarrow MP\) là đường trung bình của hình bình hành \(ACC'A'\)
\(\left. \begin{array}{l} \Rightarrow MP\parallel AA'\\AA' \subset \left( {ABA'} \right)\end{array} \right\} \Rightarrow MP\parallel \left( {ABA'} \right)\)
\(\left. \begin{array}{l}MQ\parallel \left( {ABA'} \right)\\MP\parallel \left( {ABA'} \right)\\MP,MQ \subset \left( {MPQ} \right)\end{array} \right\} \Rightarrow \left( {MPQ} \right)\parallel \left( {ABA'} \right)\)
Chọn D.
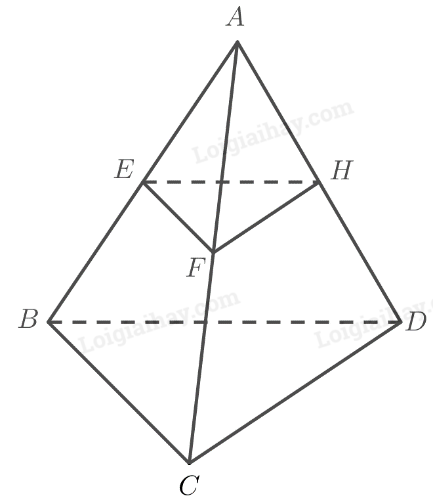
Cho tứ diện \(ABCD\) có \(E,F,H\)lần lượt là trung điểm của \(AB,AC,AD\). Chứng minh \(\left( {EFH} \right)\parallel \left( {BCD} \right)\).
Ta có: \(E\) là trung điểm của \(AB\)
\(F\) là trung điểm của \(AC\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow EF\parallel BC\\BC \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {BC{\rm{D}}} \right)\)
\(E\) là trung điểm của \(AB\)
\(H\) là trung điểm của \(AD\)
\( \Rightarrow EH\) là đường trung bình của tam giác \(ABD\)
\(\left. \begin{array}{l} \Rightarrow EH\parallel BD\\BD \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EH\parallel \left( {BC{\rm{D}}} \right)\)
Ta có:
\(\left. \begin{array}{l}EF\parallel \left( {BCD} \right)\\EH\parallel \left( {BCD} \right)\\EF,EH \subset \left( {EFH} \right)\end{array} \right\} \Rightarrow \left( {EFH} \right)\parallel \left( {BCD} \right)\)
Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\). Giả sử M, N, P lần lượt là trung điểm của các đoạn thẳng AD, BC, AC. Chứng minh:
a) M, N, P thẳng hàng
b) \(MN = \frac{1}{2}\left( {AB + CD} \right)\).
a) Vì M và P lần lượt là trung điểm của hai cạnh AD, AC nên MP là đường trung bình của tam giác ADC.
\( \Rightarrow MP\parallel AB\parallel CD\,\,\left( 1 \right)\)
Vì P và N lần lượt là trung điểm của hai cạnh AC, BC nên PN là đường trung bình của tam giác ABC.
\( \Rightarrow PN\parallel AB\parallel CD\,\,\left( 2 \right)\)
Từ (1) và (2) ta có \(MP \equiv PN\) hay ba điểm M, N, P thẳng hàng.
b) Vì MP là đường trung bình của tam giác ADC nên \(MP = \frac{1}{2}DC\).
Vì PN là đường trung bình của tam giác ABC nên \(PN = \frac{1}{2}AB\).
Ta có:
\(MN = MP + PN = \frac{1}{2}DC + \frac{1}{2}AB = \frac{1}{2}\left( {DC + AB} \right)\)
Vậy \(MN = \frac{1}{2}\left( {AB + CD} \right)\).
Cho tam giác ABC có \(AB = 4,5cm,\,\,AC = 6cm\). Các điểm M, N lần lượt thuộc các cạnh AB, AC thỏa mãn \(AM = 3cm\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng AN.
Xét tam giác ABC có \(MN\parallel BC\) nên:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (Hệ quả của định lý Thales)
\( \Rightarrow \frac{3}{{4,5}} = \frac{{AN}}{6} \Rightarrow AN = 6.3:4,5 = 4cm\).
Cho hình thang ABCD \(\left( {AB\parallel CD} \right)\) có AB = 4cm, CD = 6cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\);
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
a) Vì \(d\parallel CD\) nên \(MP\parallel CD\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{MD}} = \frac{{AP}}{{PC}}\,\,\left( 1 \right)\) (Định lý Thales)
Vì \(d\parallel AB\) nên \(PN\parallel AB\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{BN}}{{NC}} = \frac{{AP}}{{PC}}\,\,\left( 2 \right)\) (Định lý Thales)
Từ (1) và (2) ta có \(\frac{{AM}}{{MD}} = \frac{{BN}}{{NC}}\).
b) Vì \(MD = 2MA\) nên \(\frac{{AM}}{{MD}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AD}} = \frac{1}{3}\)
Xét tam giác ADC với \(MP\parallel CD\) có: \(\frac{{AM}}{{AD}} = \frac{{MP}}{{DC}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{MP}}{{DC}} = \frac{1}{3} \Rightarrow MP = \frac{1}{3}DC = 2cm\)
Vì \(\frac{{AM}}{{AD}} = \frac{1}{3} \Rightarrow \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow \frac{{PC}}{{CA}} = \frac{2}{3}\)
Xét tam giác ABC với \(PN\parallel AB\) có: \(\frac{{CP}}{{CA}} = \frac{{PN}}{{AB}}\) (Hệ quả định lý Thales)
\( \Rightarrow \frac{{PN}}{{AB}} = \frac{2}{3} \Rightarrow PN = \frac{2}{3}AB = \frac{8}{3}cm\)
Mà \(MN = MP + PM = 2 + \frac{8}{3} = \frac{{14}}{3}cm\).