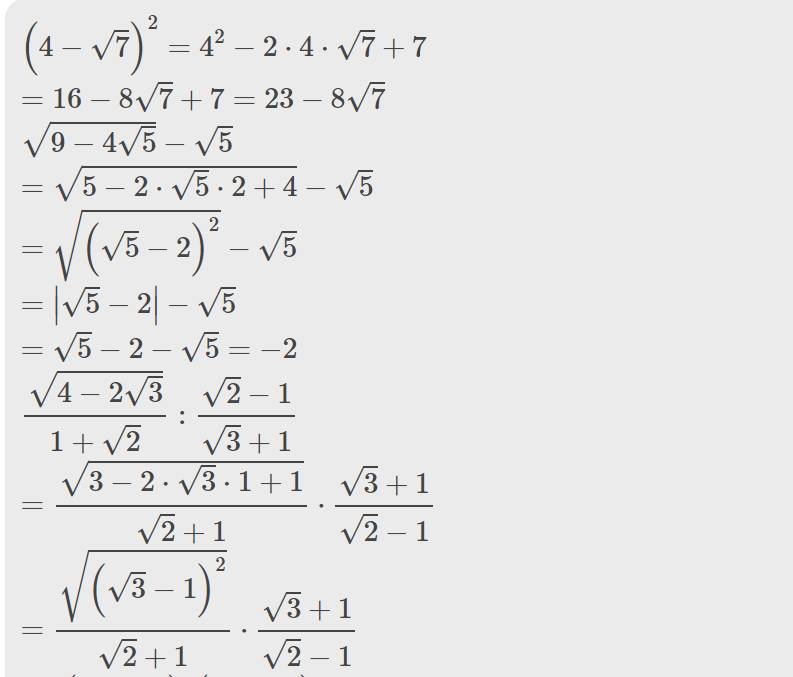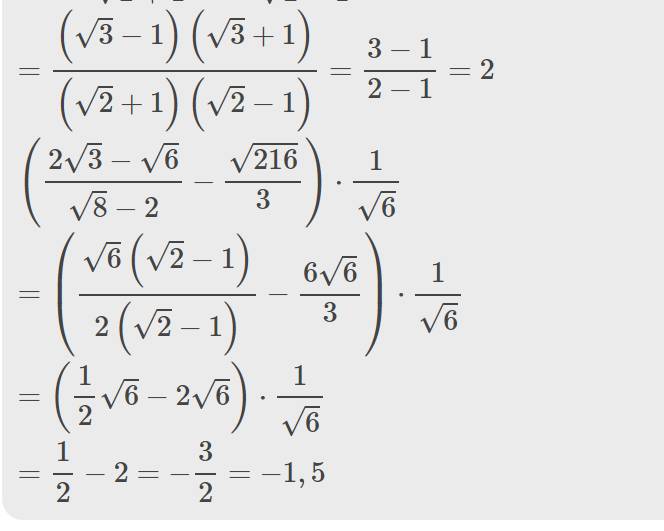C/M : Đẳng Thức \(\sqrt{9+4\sqrt{5}}\) - \(\sqrt{5}\) = 2

Những câu hỏi liên quan
Chứng minh đẳng thức sau:
\(\frac{a+\sqrt{2+\sqrt{5}}.\sqrt{\sqrt{9-4\sqrt{5}}}}{\sqrt[3]{2-\sqrt{5}}.\sqrt[3]{\sqrt{9+4\sqrt{5}}-\sqrt[3]{a^2}}+\sqrt[3]{a}}=-\sqrt[3]{a-1}\)
Chứng minh bất đẳng thức sau:
\(\left(\sqrt[3]{\sqrt{9+4\sqrt{5}}+\sqrt[3]{2+\sqrt{5}}}\right).\sqrt[3]{\sqrt{5-2}}-2,1< 0\)
Bài 1:Chứng minh các đẳng thức:
a) \(\sqrt{5}+\sqrt{3}=\sqrt{8+2\sqrt{3}}\)
b)\(\sqrt{5}+2=\sqrt{9+4\sqrt{5}}\)
Chứng minh đẳng thức
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
CM : \(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
Giải :
VT= \(\sqrt{9-4\sqrt{5}}-\sqrt{5}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\left|\sqrt{5}-2\right|-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\)
Thấy VT = VP = - 2
=> \(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\) ( đpcm )
Đúng 0
Bình luận (0)
Chứng minh đẳng thức.
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(VT=\sqrt{9-4\sqrt{5}}-\sqrt{5}=\sqrt{\left(\sqrt{5-2}\right)^2}-\sqrt{5}=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
Ta thấy VT = VF = -2
\(\Rightarrow\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\left(đpcm\right)\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)=\(\sqrt{\left(2\right)^2-2.2\sqrt{5}+5}-\sqrt{5}\)=\(\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{5}\)=\(|2-\sqrt{5}|-\sqrt{5}\)=\(\sqrt{5}-2-\sqrt{5}\)=\(-2\)=Vế Phải (điều phải chứng min)
Đúng 0
Bình luận (0)
Chứng minh đẳng thức
\(\left(4-\sqrt{7}\right)^2=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}=-1,5\)
\(\left(4-\sqrt{7}\right)^2=4^2-2\cdot4\cdot\sqrt{7}+7\)
\(=16-8\sqrt{7}+7=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{5-2\cdot\sqrt{5}\cdot2+4}-\sqrt{5}\)
\(=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}\)
\(=\left|\sqrt{5}-2\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}+1}\)
\(=\dfrac{\sqrt{3-2\cdot\sqrt{3}\cdot1+1}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}+1}\cdot\dfrac{\sqrt{3}+1}{\sqrt{2}-1}\)
\(=\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}=\dfrac{3-1}{2-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}-\dfrac{6\sqrt{6}}{3}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{1}{2}\sqrt{6}-2\sqrt{6}\right)\cdot\dfrac{1}{\sqrt{6}}\)
\(=\dfrac{1}{2}-2=-\dfrac{3}{2}=-1,5\)
Đúng 1
Bình luận (0)
Chứng minh đẳng thức
\(\left(4-\sqrt{7}\right)^2=23-8\sqrt{7}\)
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\dfrac{\sqrt{4-2\sqrt{3}}}{1+\sqrt{2}}:\dfrac{\sqrt{2}-1}{\sqrt{3}-1}=2\)
\(\left(\dfrac{2\sqrt{3}-\sqrt{6}}{\sqrt{8}-2}-\dfrac{\sqrt{216}}{3}\right).\dfrac{1}{\sqrt{6}}=-1,5\)
Chứng minh đẳng thức:
\(\sqrt{9-4\sqrt{5}}-\sqrt{5}=-2\)
\(\sqrt{23+8\sqrt{7}}-\sqrt{7=4}\)
\(\sqrt{\sqrt{5}^2-2.2\sqrt{5}+4}-\sqrt{5}=\sqrt{\left(\sqrt{5}-2\right)^2}-\sqrt{5}=\sqrt{5}-2-\sqrt{5}=-2\left(dpcm\right)\)\(\sqrt{23+8\sqrt{7}}-\sqrt{7}=\sqrt{\sqrt{7}^2+2.4\sqrt{7}+16}-\sqrt{7}\)\(=\sqrt{\left(\sqrt{7}+4\right)^2}-\sqrt{7}=\sqrt{7}+4-\sqrt{7}=4\left(DPCM\right)\)
Đúng 0
Bình luận (0)
cmr các đẳng thức :
1/\(\sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}=3\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}\)
2/\(\frac{\sqrt[4]{5}+1}{\sqrt[4]{5}-1}=\sqrt[4]{\frac{3+2\sqrt[4]{5}}{3-2\sqrt[4]{5}}}\)
3/\(\sqrt[3]{\sqrt[3]{2}-1}=\sqrt[3]{\frac{1}{9}}-\sqrt[3]{\frac{2}{9}}+\sqrt[3]{\frac{4}{9}}\)
giúp mik vs mik cần gấp lắm
CM các đẳng thức sau:
a) \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}=9\)
b) \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\sqrt{6}\)
c) \(\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=8\)
a) \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}=9\)
Ta có : VT = \(2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}\)
\(\Leftrightarrow VT=9\) \(=VP\)
Vậy.........
b) \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\sqrt{6}\)
<=> \(\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2=6\)
Ta có : VT = \(2+\sqrt{3}+2-\sqrt{3}+2\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
= \(4+2\sqrt{4-3}=4+2=6\)
=> VT = VP
Vậy.....
c) \(\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=8\)
Ta có : VT = \(\dfrac{\sqrt{4}}{\sqrt{\left(2-\sqrt{5}\right)^2}}-\dfrac{\sqrt{4}}{\sqrt{\left(2+\sqrt{5}\right)^2}}\)
= \(\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{2+\sqrt{5}}=\dfrac{4+2\sqrt{5}-2\sqrt{5}+4}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}\)
= \(\dfrac{8}{5-4}=8\)
=> VT = VP
Vậy....
Đúng 0
Bình luận (0)
a) Biến đổi vế trái ta có:
VT= \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}\)
= \(2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}\)
= 9 = VP
Vậy đẳng thức đc chứng minh
b) Đặt vế trái = A = \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\)
\(A^2=\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)^2\)
\(A^2=2+\sqrt{3}+2-\sqrt{3}+2.\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\)
\(A^2=4+2.\sqrt{4-3}=4+2.1=6\)
\(\Rightarrow A=\sqrt{6}=VP\)
Vậy đẳng thức đc chứng minh
Đúng 0
Bình luận (0)
a) \(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}=9\)
BĐVT ta có:
\(2\sqrt{2}\left(\sqrt{3}-2\right)+\left(1+2\sqrt{2}\right)^2-2\sqrt{6}=2\sqrt{6}-4\sqrt{2}+1+4\sqrt{2}+8-2\sqrt{6}=9=VP\)
Vậy đẳng thức đã được C/m
b) \(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\sqrt{6}\)
BĐVT ta có:
\(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}=\dfrac{\sqrt{2}\left(\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\right)}{\sqrt{2}}\)
\(=\dfrac{\sqrt{4+2\sqrt{3}}+\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{3+1}\right)^2}+\sqrt{\left(\sqrt{3-1}\right)^2}}{\sqrt{2}}\)
\(=\dfrac{\left|\sqrt{3+1}\right|+\left|\sqrt{3-1}\right|}{\sqrt{2}}=\dfrac{\sqrt{3+1}+\sqrt{3-1}}{\sqrt{2}}=\dfrac{2\sqrt{3}}{\sqrt{2}}=\sqrt{6}=VP\)
Vậy đẳng thức đã được C/m
c) \(\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=8\)
BĐVT ta có:
\(\sqrt{\dfrac{4}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{4}{\left(2+\sqrt{5}\right)^2}}=\sqrt{\dfrac{2^2}{\left(2-\sqrt{5}\right)^2}}-\sqrt{\dfrac{2^2}{\left(2+\sqrt{5}\right)^2}}\)
\(=\dfrac{2}{\left|2-\sqrt{5}\right|}-\dfrac{2}{\left|2+\sqrt{5}\right|}=\dfrac{2}{\sqrt{5}-2}-\dfrac{2}{\sqrt{5}+2}=\dfrac{2\left(\sqrt{5}+2\right)-2\left(\sqrt{5}-2\right)}{\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)}\)
\(=\dfrac{2\sqrt{5}+4-2\sqrt{5}+4}{5-4}=8=VP\)
Vậy đẳng thức đã dược C/m
Đúng 0
Bình luận (0)