Tìm mối liên hệ giữa hành trình pít tông S và bán kính quay R của trục khuỷu.
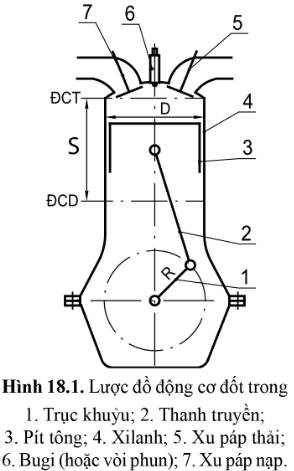
Quan hệ giữa hành trình pit-tông và bán kính quay của trục khuỷu là:
A. S = R
B. S = 1 R
C. S = 2 R
D. S = R 2
Quan hệ giữa hành trình pit-tông và bán kính quay của trục khuỷu là:
A. S = R
B. S = 1/R
C. S = 2R
D. S = R/2
Giải thích vì sao trục khuỷu quay được n vòng thì pít tông đi được 2n hành trình
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho \(\alpha \) là góc quay của trục khuỷu, O là vị trí của pít – tông khi \(\alpha = \frac{\pi }{2}\) và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.
a) Biết IA = 8cm, viết công thức tính tọa độ \({x_M}\)của điểm M trên trục Ox theo \(\alpha \).
b) Ban đầu \(\alpha = 0\). Sau 1 phút chuyển động, \({x_M}\)= – 3cm. Xác định\({x_M}\) sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười
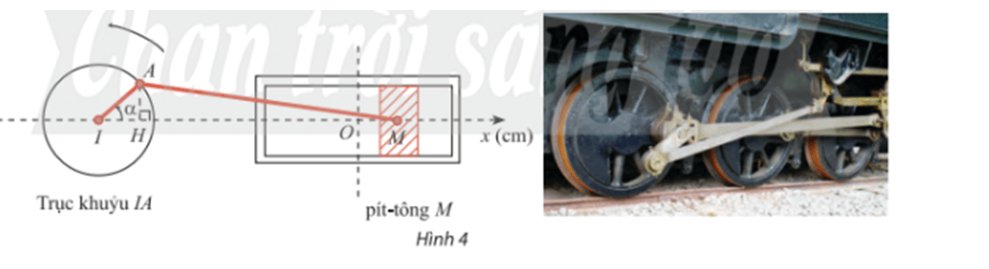
a, Tại \(\alpha = \frac{\pi }{2}\) thì H trùng I, M trùng O nên MH = OI do đó OM = IH.
Xét tam giác AHI vuông tại H có: \(IH = cos\alpha .IA = 8cos\alpha .\)
\( \Rightarrow {x_M} = OM = IH = 8cos\alpha \)
b, Sau khi chuyển động được 1 phút, trục khuỷu quay được một góc là \(\alpha \)
Khi đó \({x_M} = - 3cm \Rightarrow cos\alpha = - \frac{3}{8}\)
Sau khi chuyển động 2 phút, trục khuỷu quay được một góc \(2\alpha \), nên:
\({x_M} = 8cos2\alpha = 8\left( {2{{\cos }^2}\alpha - 1} \right)\)\( = 8\left( {2{{\left( { - \frac{3}{8}} \right)}^2} - 1} \right) \approx - 5,8 cm\)
Pít-tông của một động cơ đốt trong dao động trên một đoạn thẳng dài 16cm và làm cho trục khuỷu của động cơ quay đều (Hình 1.5). Xác định biên độ dao động của một điểm trên mặt pít-tông.
Dao động trên một đường thẳng dài `16 cm`
`=>L=16 (cm)`
Mà `A=L/2`
`=>A=16/2=8` (cm)
Quan sát Hình 17.4 và cho biết: Theo chiều chuyển động quay của trục khuỷu (6), pít tông (4) đang dịch chuyển như thế nào?
- Khi nào pít tông (4) đổi chiều chuyển động?
- Hãy mô tả sự thay đổi thể tích giới hạn bởi đỉnh pít tông và không gian phía trên của xi lanh.
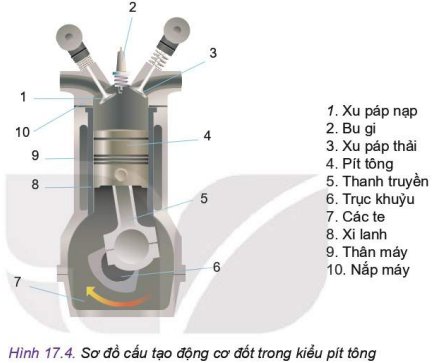
- Pít tông (4) đang dịch chuyển lên trên. Khi pit tông dịch chuyển lên vị trí cao nhất sẽ đổi chiều chuyển động, và sau đó khi pit tông dịch chuyển xuống vị trí thấp nhất sẽ lại đổi chiều chuyển động.
- Mô tả sự thay đổi thể tích giới hạn bởi đỉnh pít tông và không gian phía trên của xi lanh:
+ Thể tích lớn nhất khi trục khuỷu quay ở vị trí số 6 của kim đồng hồ.
+ Thể tích nhỏ nhất khi trục khuỷu quay ở vị trí số 12 của kim đồng hồ.
Quan sát Hình 18.2 và cho biết hình nào có đỉnh pít tông xa tâm trục khuỷu nhất và hình nào có đỉnh pít tông gân tâm trục khuỷu nhất?
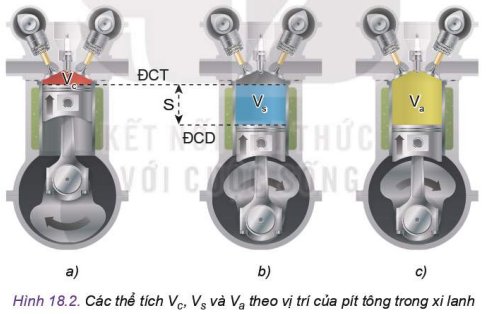
- Hình a có đỉnh pit tông ở xa tâm trục khuỷu nhất.
- Hình b, c có đỉnh pit tông gần tâm trục khuỷu nhất.
Em hãy quan sát Hình 18.1 và cho biết nếu trục khuỷu quay theo chiều mũi tên, pít tông sẽ chuyển động lên trên hay xuống dưới; thể tích, nhiệt độ và áp suất phía trên đỉnh pít tông (phần tô màu xanh) thay đổi như thế nào?
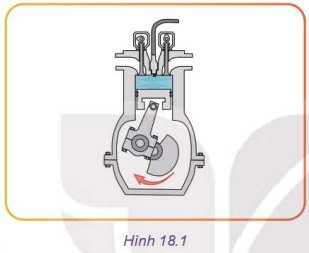
Trục khuỷu quay theo chiều mũi tên, pít tông sẽ chuyển động lên trên; thể tích giảm dần, nhiệt độ và áp suất phía trên đỉnh pít tông tăng dần.
Khi pit-tông dịch chuyển được 1 hành trình thì trục khuỷu sẽ quay góc:
A. 90ᵒ
B. 180ᵒ
C. 360ᵒ
D. 720ᵒ