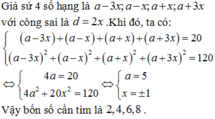tk

Gọi 4 số nguyên dương lần lượt là a,a+1,a+2,a+3 
Ta có:a.(a+1).(a+2).(a+3)=120 
<=>(a.(a+3)).((a+1).(a+2))=120 
<=>(a^2+3a).(a^2+3a+2)=120 
<=>(a^2+3a+1-1).(a^2+3a+1+1)=120 
Đặt;x=a^2+3a+1 
Lại có:(x-1).(x-1)=120 
<=>x^2-1^2=120 
<=>x^2=121 
<=>x=11 
<=>a^2+3a+1=11 
<=>a^2+3a-10=0 
<=>(a-2).(a+5)=10 
<=>a=2 
Vậy 4 số nguyên dương liên tiếp đó là 2;3;4;5

Gọi 4 số nguyên dương liên tiếp theo thứ tự tăng dần lần lượt là: a,a+1,a+2,a+3

Theo đề bài ta có:

\(a\left(a+1\right)\left(a+2\right)\left(a+3\right)=120\)

\(\Leftrightarrow a^4+6a^3+11a^2+6a-120=0\)

\(\Leftrightarrow\left(a-2\right)\left(a+5\right)\left(x^2+3x+12\right)=0\)

\(\Leftrightarrow a=2\)( do a là số nguyên dương)

Vậy 4 số nguyên dương liên tiếp đó lần lượt là: \(2,3,4,5\)

Gọi 4 số nguyên dương lần lượt là a,a+1,a+2,a+3 
Ta có:a.(a+1).(a+2).(a+3)=120 
<=>(a.(a+3)).((a+1).(a+2))=120 
<=>(a^2+3a).(a^2+3a+2)=120 
<=>(a^2+3a+1-1).(a^2+3a+1+1)=120 
Đặt;x=a^2+3a+1 
Lại có:(x-1).(x-1)=120 
<=>x^2-1^2=120 
<=>x^2=121 
<=>x=11 
<=>a^2+3a+1=11 
<=>a^2+3a-10=0 
<=>(a-2).(a+5)=10 
<=>a=2 
Vậy 4 số nguyên dương liên tiếp đó là 2;3;4;5

Giả sử số hạng đầu tiên của số nguyên dương đó là x;(x>0)

Yêu cầu bài toán ⇔x(x+1)(x+2)(x+3)=120
⇔x4+6x3+11x2+6x−120=0

⇔(x2+3x−10)(x2+3x+12)=0

⇒x=2

Vậy 44 số nguyên dương liên tiếp biết tích của chúng bằng 120: 2;3;4;5

Ta thấy 120 có các ước như sau :

A = { 1 ; 2 ; 4 ; 8 ; 16 ; 60 ; 30 ; 20 ; 10 ; 40 ; 120 ; 5 }

Đặt 4 số lần lượt là a , b , c , d.

Ta thấy : 120 = 60 . 2 = 10 . 6 . 2 = 10 . 3 . 2 . 2 = 10 . 3 . 4 = 5 . 2 . 3 . 4

Vậy 4 số cần tìm là 5 , 2 , 3 và 4.

Gọi 4 số nguyên dương cần tìm là x, x+1, x+2, x+3 ( x > 0 )

Tích của chúng = 120

=> x( x + 1 )( x + 2 )( x + 3 ) = 120

=> [ x( x + 3 ) ][ ( x + 1 )( x + 2 ) ] - 120 = 0

=> ( x² + 3x )( x² + 3x + 2 ) - 120 = 0 (*)

Đặt t = x² + 3x 

(*) <=> t( t + 2 ) - 120 = 0

     <=> t² + 2t - 120

     <=> t² - 10t + 12t - 120 = 0

     <=> t( t - 10 ) + 12( t - 10 ) = 0

     <=> ( t - 10 )( t + 12 ) = 0

     <=> ( x² + 3x - 10 )( x² + 3x + 12 ) = 0

Vì x² + 3x + 12 = ( x² + 3x + 9/4 ) + 39/4 = ( x + 3/2 )² + 39/4 ≥ 39/4 > 0 ∀ x

=> x² + 3x - 10 = 0

=> x² - 2x + 5x - 10 = 0

=> x( x - 2 ) + 5( x - 2 ) = 0

=> ( x - 2 )( x + 5 ) = 0

=> x = 2 ( tm ) hoặc x = -5 ( ktm )

=> x + 1 = 3 ; x + 2 = 4 ; x + 3 = 5

Vậy bốn số cần tìm là 2 ; 3 ; 4 ; 5 

Hơi dài một tí (:

Gọi 4 số nguyên dương cần tìm là a , a + 1 , a + 2 , a + 3

Theo đề bài ta có : a(a + 1)(a + 2)(a + 3) = 120

=> a(a + 3)(a + 1)(a + 2) = 120

=> (a² + 3a)(a² + 3a + 2) = 120

Đặt a² + 3a = t

=> t(t + 2) = 120

=> t² + 2t = 120

=> t² + 2t - 120 = 0

=> (t² + 2t +1) - 121 = 0

=> (t + 1)² - 121 = 0

=> (t + 1)² = 121 = 11²

=> t + 1 = 11 => t = 10 

+) Lại có : a² + 3a = t

=> a² + 3a - 10 = 0

=> a² - 2a + 5a - 10 = 0

=> a(a - 2) + 5(a - 2) = 0

=> (a - 2)(a + 5) = 0

=> a = 2 hoặc a = -5

Loại a = -5 vì 4 số liên tiếp đều là nguyên dương

+) a + 1 = 2 + 1 = 3

+) a + 2 = 2 + 2 = 4

+) a + 3 = 2 + 3 = 5

Vậy : ....

Ta có 3.4.5.6=120.3>120
→→ 4 số nguyên liên0 tiếp này có số bé nhất <3
mà 1.2.3.4=24 <120
→4→4 số nguyên lien tiếp này có số bé nhất >1
→4→4 só đó là2,3,4,52,3,4,5

k mk nha!!

2x3x4x5=120.

Ta có: \(3.4.5.6=120.3>120\)

\(\rightarrow\)4 số nguyên tiếp này có số bé nhất bé hơn 3 mà \(1.2.3.4=24< 120\)

\(\rightarrow\)4 số nguyên liên tiếp này có số bé nhất > 1

\(\rightarrow\)4 số đó là \(2;3;4;5\)

tổng bằng 14

Ta có a.b.c = a+b+c 
Giả sử a = b = c ta có a^3 = 3a => a^2 = 3. Ptrình này không cho nghiệm nguyên dương, nên a; b; c là 3 số nguyên dương phân biệt. 
Tìm các số nguyên dương: 
Giả sử a là số lớn nhất trong 3 số. Ta có a + b + c = a.b.c < 3a. Hay tích b.c <3. Vì a; b; c là các số nguyên dương; b.c <3. Do b;c nguyên dương nên tích b,c nguyên dương hay b.c = 1 hoặc b.c =2. Mặt khác chứng minh được b khác c nên b và c chỉ có thể là 1 và 2. Ở đây ta giả sử c là 1. thì b là 2. (b khác 2 thì tích b.c > 3 là vô lý). 

Vậy ta có 1 + 2 + a = 1.2.a hay 3+a = 2a => a = 3. 
______________________________________________
li-ke cho mk nhé bn nguyễn thị huyền thương 

\(Ta\)\(có\): \(5n^3+15n+10n=5n\left(n^2+3n+2\right)\)

                 \(=5n\left[\left(n^2+n\right)+\left(2n+2\right)\right]=5n\left[n\left(n+1\right)+2\left(n+1\right)\right]\)

                 \(=5n\left(n+1\right)\left(n+2\right)\)

\(Vì\)\(n\left(n+1\right)\left(n+2\right)⋮6\)\(và\) \(5⋮5\)

\(nên\) \(5n\left(n+1\right)\left(n+2\right)⋮\left(5.6\right)\Rightarrow5n\left(n+1\right)\left(n+2\right)⋮30\left(đpcm\right)\)

bạn giúp mk bài 2 nx

Bài 1:

 \(5n^3+15n^2+10n=5n\left(n^2+3n+2\right)=5n\left[\left(n^2+n\right)+\left(2n+2\right)\right]\)

\(=5n\left[n\left(n+1\right)+2\left(n+1\right)\right]=5n\left(n+1\right)\left(n+2\right)\)

Vì \(n\), \(n+1\)là 2 số nguyên liên tiếp 

\(\Rightarrow n\left(n+1\right)⋮2\)\(\Rightarrow n\left(n+1\right)\left(n+2\right)⋮2\)(1)

Vì \(n\), \(n+1\), \(n+2\)là 3 số nguyên liên tiếp

\(\Rightarrow n\left(n+1\right)\left(n+2\right)⋮3\)(2)

Vì \(\left(2;3\right)=1\)(3)

Từ (1), (2) và (3) \(\Rightarrow n\left(n+1\right)\left(n+2\right)⋮6\)

\(\Rightarrow5n\left(n+1\right)\left(n+2\right)⋮30\)

\(\Rightarrow5n^3+15n^2+10n⋮30\)( đpcm )

Bài 2:

Gọi 4 số nguyên dương liên tiếp là \(a\), \(a+1\), \(a+2\), \(a+3\)( \(a\inℕ^∗\))

Theo bài, ta có: \(a\left(a+1\right)\left(a+2\right)\left(a+3\right)=120\)

\(\Leftrightarrow a\left(a+3\right)\left(a+1\right)\left(a+2\right)=120\)

\(\Leftrightarrow\left(a^2+3a\right)\left(a^2+3a+2\right)=120\)

Đặt \(a^2+3a+1=t\)

\(\Rightarrow\left(t-1\right)\left(t+1\right)=120\)\(\Leftrightarrow t^2-1-120=0\)

\(\Leftrightarrow t^2-121=0\)\(\Leftrightarrow\left(t-11\right)\left(t+11\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}t-11=0\\t+11=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}t=11\\t=-11\end{cases}}\)

+) TH1: Nếu \(t=-11\)\(\Rightarrow a^2+3a+1=-11\)

\(\Leftrightarrow a^2+3a+12=0\)( không có nghiệm nguyên )

+) TH2: Nếu \(t=11\)\(\Rightarrow a^2+3a+1=11\)

\(\Leftrightarrow a^2+3a-10=0\)\(\Leftrightarrow\left(a-2\right)\left(a+5\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}a-2=0\\a+5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}a=2\\a=-5\end{cases}}\)

Vì \(a\inℕ^∗\)\(\Rightarrow a=2\)thỏa mãn đề bài 

Vậy 4 số nguyên dương cần tìm là 2, 3, 4, 5

Chọn đáp án B