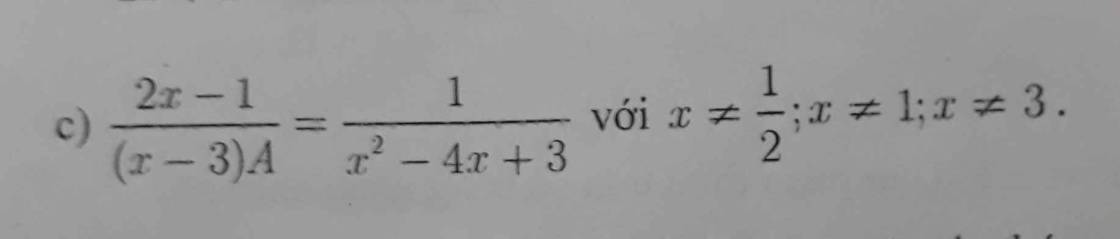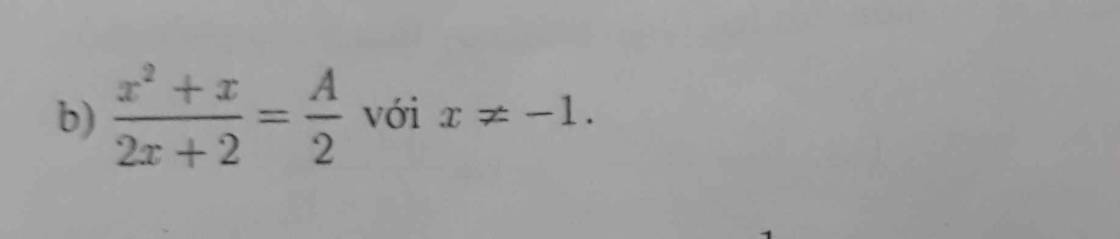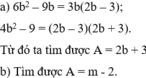Tìm đa thức A trong mỗi đẳng thức sau: a) b) c)

Những câu hỏi liên quan
Tìm đa thức A trong mỗi đẳng thức sau:
\(b,\dfrac{x^2+x}{2x+2}=\dfrac{A}{2}\\ \Rightarrow2\left(x^2+x\right)=A.\left(2x+2\right)\\ \Rightarrow A=\dfrac{2\left(x^2+x\right)}{2x+2}=\dfrac{2x\left(x+1\right)}{2\left(x+1\right)}=x\)
Vậy \(A=x\)
\(c,\dfrac{2x-1}{\left(x-3\right).A}=\dfrac{1}{x^2-4x+3}\\ \Leftrightarrow\dfrac{2x-1}{\left(x-3\right).A}=\dfrac{1}{\left(x-1\right)\left(x-3\right)}\\ \Rightarrow\left(x-3\right).A=\left(2x-1\right)\left(x-1\right)\left(x-3\right)\\ \Leftrightarrow A=\left(2x-1\right)\left(x-1\right)\\=2x^2-x-2x+1\\ =2x^2-3x+1\)
Vậy \(A=2x^2-3x+1\)
@seven
Đúng 2
Bình luận (1)
Tìm đa thức A trong mỗi đẳng thức sau:a)
A
2
x
−
3
2
x
2
+
3
x
4
x
2
−
9
với x
≠
±...
Đọc tiếp
Tìm đa thức A trong mỗi đẳng thức sau:
a) A 2 x − 3 = 2 x 2 + 3 x 4 x 2 − 9 với x ≠ ± 3 2 ;
b) b 2 − 3 b 2 b 2 − 3 b − 9 = b 2 + 3 b A với b ≠ − 3 2 và b ≠ ± 3 .
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
A
2
x
-
1
6
x
2
+
3
x
4
x
2
-
1
Đọc tiếp
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
A 2 x - 1 = 6 x 2 + 3 x 4 x 2 - 1
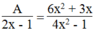 ⇒
A
4
x
2
-
1
=
2
x
-
1
6
x
2
+
3
x
⇒
A
4
x
2
-
1
=
2
x
-
1
6
x
2
+
3
x
⇒ A(2x – 1)(2x + 1) = (2x – 1).3x(2x + 1) ⇒ A = 3x
Vậy 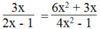
Đúng 0
Bình luận (0)
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
x
2
-
2
x
2
x
2
-
3
x
-
2
x
2
+...
Đọc tiếp
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
x 2 - 2 x 2 x 2 - 3 x - 2 = x 2 + 2 x A
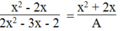 ⇒
x
2
-
2
x
.
A
=
2
x
2
-
3
x
-
2
x
2
+
2
x
⇒
x
2
-
2
x
.
A
=
2
x
2
-
3
x
-
2
x
2
+
2
x
⇒ x x - 2 . A = 2 x 2 - 4 x + x - 2 . x x + 2
⇒ x x - 2 . A = 2 x x - 2 + x - 2 . x x + 2
⇒ x(x – 2).A = (x – 2)(2x + 1).x.(x + 2)
⇒ A = (2x + 1)(x + 2) = 2 x 2 + 4 x + x + 2 = 2 x 2 + 5 x + 2
Vậy 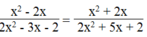
Đúng 0
Bình luận (0)
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
4 x 2 - 3 x - 7 A = 4 x - 7 2 x + 3
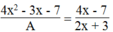 ⇒
4
x
2
-
3
x
-
7
2
x
+
3
=
A
4
x
-
7
⇒
4
x
2
-
3
x
-
7
2
x
+
3
=
A
4
x
-
7
⇒ 4 x 2 + 4 x - 7 x - 7 2 x + 3 = A 4 x - 7
⇒ [4x(x + 1) – 7(x + 1)](2x+ 3) = A(4x - 7)
⇒ (x + 1)(4x – 7)(2x + 3) = A(4x – 7)
⇒ A = (x + 1)(2x + 3) = 2 x 3 + 3 x + 2 x + 3 = 2 x 2 + 5 x + 3
Vậy 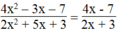
Đúng 0
Bình luận (0)
Tìm đa thức B trong mỗi đẳng thức sau:a)
2
y
−
1
(
y
−
3
)
B
1
y
2
−
4
y
+
3
với
y...
Đọc tiếp
Tìm đa thức B trong mỗi đẳng thức sau:
a) 2 y − 1 ( y − 3 ) B = 1 y 2 − 4 y + 3 với y ≠ 1 2 ; y ≠ 1 và y ≠ 3 ;
b) a − 1 a 2 + 2 a + 4 = B a 3 − 8 và a ≠ 2 .
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
4
x
2
-
7
x
+
3
x
2
-
1
A
x
2
+...
Đọc tiếp
Dùng định nghĩa hai phân thức bằng nhau, hãy tìm đa thức A trong mỗi đẳng thức sau:
4 x 2 - 7 x + 3 x 2 - 1 = A x 2 + 2 x + 1
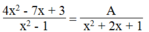 ⇒
4
x
2
-
7
x
+
3
x
2
+
2
x
+
1
=
A
x
2
-
1
⇒
4
x
2
-
7
x
+
3
x
2
+
2
x
+
1
=
A
x
2
-
1
⇒ 4 x 2 - 4 x - 3 x + 3 x + 1 2 = A x + 1 x - 1
⇒ 4 x x - 1 - 3 x - 1 . x + 1 2 = A . x + 1 x - 1
⇒ x - 1 4 x - 3 x + 1 2 = A x + 1 x - 1
⇒ A = 4 x - 3 x + 1 = 4 x 2 + 4 x - 3 x - 3 = 4 x 2 + x - 3
Vậy 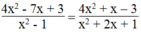
Đúng 0
Bình luận (0)
Trong mỗi đẳng thức sau, hãy tìm đa thức M phù hợp:a)
3
y
2
+
6
y
(
y
−
1
)
M
3
y
y
−
1
với
y...
Đọc tiếp
Trong mỗi đẳng thức sau, hãy tìm đa thức M phù hợp:
a) 3 y 2 + 6 y ( y − 1 ) M = 3 y y − 1 với y ≠ − 2 và y ≠ 1 ;
b) − 2 a 2 + 4 ab + 2 b 2 a + b = M b 2 − a 2 với a ≠ ± b .
Tìm đa thức A thỏa mãn mỗi đẳng thức sau:a)
6
b
2
−
9
b
4
b
2
−
9
3
b
A
với
b
≠
±
3
2
;...
Đọc tiếp
Tìm đa thức A thỏa mãn mỗi đẳng thức sau:
a) 6 b 2 − 9 b 4 b 2 − 9 = 3 b A với b ≠ ± 3 2 ;
b) n − m 2 − m = m − n A với m ≠ 2 .