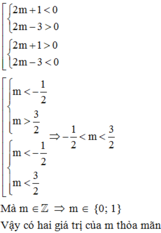Xét pt: \(x^2-2mx+m^2-2m+3=0\) (1)

\(\Delta'=m^2-\left(m^2-2m+3\right)=2m-3\) 

- Nếu \(2m-3< 0\Leftrightarrow m< \dfrac{3}{2}\Rightarrow\left(1\right)\) vô nghiệm hay hàm xác định trên R

- Nếu \(2m-3=0\Leftrightarrow m=\dfrac{3}{2}\Rightarrow\left(1\right)\) có nghiệm kép \(x=\dfrac{3}{2}\) hay TXĐ của hàm: \(D=R\backslash\left\{\dfrac{3}{2}\right\}\)

- Nếu \(2m-3>0\Leftrightarrow m>\dfrac{3}{2}\Rightarrow\left(1\right)\) có 2 nghiệm pb \(x_{1,2}=m\pm\sqrt{2m-3}\) hay TXĐ của hàm là: \(D=R\backslash\left\{m-\sqrt{2m-3};m+\sqrt{2m-3}\right\}\)

Hoành độ Giao điểm chính là nghiệm của D=P vậy ta xem nó có bao nhiêu nghiệm

x^2=2x+m-3

(x-1)^2=m-4

Nếu m=4 => có một nghiệm x=1 có 1 giao điểm 

nếu m<4 => không tồn tại x => không có giao điểm

m>4 => \(\orbr{\begin{cases}x=1-\sqrt{m-4}\\x=1+\sqrt{m-4}\end{cases}}\) => có 2 điểm

Thank you

Lời giải:

PT hoành độ giao điểm:

$x^2-2mx-(2m+1)=0(*)$

Để (P) và (d) cắt nhau tại 2 điểm pb có hoành độ $x_1,x_2$ thì PT $(*)$ phải có 2 nghiệm pb $x_1,x_2$

$\Leftrightarrow \Delta'=m^2+2m+1>0\Leftrightarrow (m+1)^2>0$

$\Leftrightarrow m\neq -1$
Áp dụng định lý Viet: $x_1+x_2=2m; x_1x_2=-(2m+1)$

Khi đó:

$\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1$

$\Leftrightarrow \sqrt{2m}+\sqrt{3-2m-1}=2m+1$
\(\Leftrightarrow \left\{\begin{matrix} 0\leq m< 1\\ \sqrt{2m}+\sqrt{2(1-m)}=2m+1\end{matrix}\right.\)

Bình phương 2 vế dễ dàng giải ra $m=\frac{1}{2}$ (thỏa)

Phương trình hoành độ giao điểm của \(\left(d\right)\) và \(\left(P\right)\) là: 

\(x^2=2mx+3\Leftrightarrow x^2-2mx-3=0\) (1) 

Phương trình (1) có hệ số \(a.c=1.\left(-3\right)=-3< 0\) nên (1) luôn có hai nghiệm phân biệt \(x_1,x_2\).

Theo hệ thức Viete ta có: 

\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-3\end{matrix}\right.\)

Ta có: \(\left|x_1\right|+3\left|x_2\right|=6\)

Ta có hệ: 

\(\left\{{}\begin{matrix}x_1x_2=-3\\\left|x_1\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\\left|\dfrac{3}{x_2}\right|+3\left|x_2\right|=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{3}{x_2}\\x_2^2-2\left|x_2\right|+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x_2=-1,x_1=3\\x_2=1,x_1=-3\end{matrix}\right.\)

Với \(x_1=3,x_2=-1\Rightarrow x_1+x_2=2\Rightarrow m=1\).

Với \(x_1=-3,x_2=1\Rightarrow x_1+x_2=-2\Rightarrow m=-1\)

Phương trình hoành độ giao điểm của $\left(d\right)$ và $\left(P\right)$ là: 

$x^2=2mx+3\iff x^2-2mx-3=0$ (1) 

Phương trình (1) có hệ số $a.c=1.\left(-3\right)=-3<0$ nên (1) luôn có hai nghiệm phân biệt $x_1,x_2$.

Theo hệ thức Viete ta có: 

$\{\begin{array}{c}{x}_1+x_2=2m\\ x_1{x}_2=-3\end{array}$

Ta có: $\left|x_1\right|+3\left|x_2\right|=6$

Ta có hệ: 

{x1x2=−3|x1|+3|x2|=6⇔⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x1=−3x2∣∣∣3x2∣∣∣+3|x2|=6⇔⎧⎪⎨⎪⎩x1=−3x2x22−2|x2|+1=0{x1x2=−3|x1|+3|x2|=6⇔{x1=−3x2|3x2|+3|x2|=6⇔{x1=−3x2x22−2|x2|+1=0

$\iff [\begin{array}{c}{x}_2=-1,x_1=3\\ x_2=1,x_1=-3\end{array}$

Với $x_1=3,x_2=-1\Rightarrow x_1+x_2=2\Rightarrow m=1$.

Với $x_1=-3,x_2=1\Rightarrow x_1+x_2=-2\Rightarrow m=-1$

Đáp án C

- Xét phương trình hoành độ giao điểm : \(x^2=2mx-2m+3\)

\(\Leftrightarrow x^2-2mx+2m-3=0\left(I\right)\)

- Xét thấy để P và d cắt nhau tại hai điểm phân biệt khi PT ( I ) có hai nghiệm phân biệt .

\(\Leftrightarrow\Delta^,=b^{,2}-ac=m^2-\left(2m-3\right)>0\)

\(\Leftrightarrow m^2-2m+3>0\)

Mà \(m^2-2m+3=m^2-2m+1+2=\left(m+1\right)^2+2\ge2>0\forall m\in R\)

Vậy ... ĐPCM