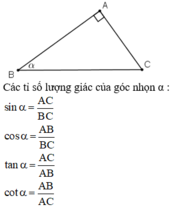
Cho góc nhọn α. Tính tỉ số lượng giác còn lại nếu cotα= 40/9

Những câu hỏi liên quan
10, Cho t/giác ABC vuông tại A có ^ABC= 40. Tính tỉ số lượng giác của ABC.
14, Cho α = 2. Tính các lượng giác còn lại của góc α biết góc α là góc nhọn.
chỉ rõ hộ mk từng cách giải đc ko ạ?
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:
t
g
α
sin
α
cos
α
,
c
o
t
α
cos
α
sin
α
,
t
a
α
.
c
o...
Đọc tiếp
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:
t g α = sin α cos α , c o t α = cos α sin α , t a α . c o t g α = 1
Gợi ý: Sử dụng định lí Pitago.
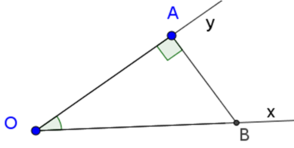
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
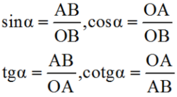
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A có góc nhọn (ABC) ̂ = α. Hãy nhắc lại định nghĩa các tỉ số lượng giác của góc nhọn α đã học ở lớp 9.
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
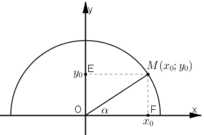
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho 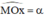
Khi đó ta có:
sin α = y0
cos α = x0
tan α = y0 / x0
cot α = x0 / y0
b) Gọi E, F là hình chiếu của M trên Oy, Ox.
Khi α < 90º thì x0 > 0, y0 > 0
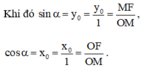
Đúng 0
Bình luận (0)
Cho α là góc nhọn, sinα = 1/2.Tính cosα;tanα;cotα
Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
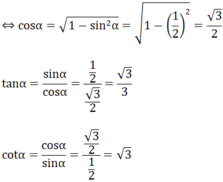
Đúng 0
Bình luận (0)
Tính các giá trị lượng giác của góc α, biết
cotα = 4tanα khi π/2 < α < π
Với π/2 < α < π thì sinα > 0, cosα < 0, tanα < 0
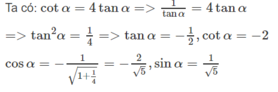
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông A, có sin = 0,6. Tính tỉ số lượng giác góc nhọn còn lại
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
Cho góc nhọn α. CMR:
a) sinα< tanα
b) cosα< cotα
b)
Có: \(cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
Vì $\alpha $ là góc nhọn nên `0<sin\alpha<1`
\(\Rightarrow\dfrac{cos\alpha}{sin\alpha}>\dfrac{cos\alpha}{1}=cos\alpha\)
Vậy \(cos\alpha< cot\alpha\)
Đúng 2
Bình luận (1)