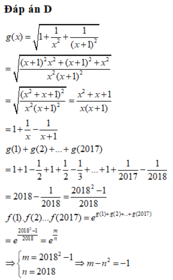tính A = ( m x1 - m : 1 ) x 2017 x 2018 ( m là số tự nhiên )

Những câu hỏi liên quan
Cho hàm số
f
(
x
)
e
1
+
1
x
2
+
1
(
x
+...
Đọc tiếp
Cho hàm số f ( x ) = e 1 + 1 x 2 + 1 ( x + 1 ) 2 , biết rằng f ( 1 ) . f ( 2 ) . f ( 3 ) . . . f ( 2017 ) = e m n với m, n là các số tự nhiên và m 2 tối giản. Tính m - n 2
A. m - n 2 = 2018
B. m - n 2 = 1
C. m - n 2 = -2018
D. m - n 2 = -1
a) Cho \(a,b,c\in R\)thỏa \(a+b+c=2018\)
Tính \(M=\frac{1}{a^{2107}}+\frac{1}{b^{2017}}+\frac{1}{c^{2017}}\)
b)Tìm số tự nhiên x,y thỏa \(5^x-2^y=1\)
MONG CÁC BẠN ZẢI NHANH ZÚP MK ĐANG CẦN GẤP
cho x, y là các số tự nhiên lớn hơn 1 thỏa mãn x^2017=y^2018. Hãy tìm số tự nhiên x, biết y là số tự nhiên nhỏ nhất.
Ai đúng, tick luôn
do y la so tu nhien nho nhat nen y=0
=>y^2018=0
=>x^2017=0
=>x=0
Đúng 0
Bình luận (0)
tính: m = 2017 x 2016+2018/2016 x 2017+4033 vậy m = …..
Cho M=(x^2+4)/(x+5). Hỏi có bao nhiêu số tự nhiên x thỏa mãn 1<=x<=2017 sao cho M là phân số chưa tối giản
Cho M = (x^2+4)/(x+5). Hỏi có bao nhiêu số tự nhiên x thỏa mãn 1<=x<=2017 sao cho M là phân số chưa tối giản
, Cho M=(x^2+4)/(x+5). Hỏi có bao nhiêu số tự nhiên x thỏa mãn 1≤x≤2017 sao cho M là phân số chưa tối giản
1)Tìm số tự nhiên x ,biết:
6+3x+2=87
2)Tìm số tự nhiên x, biết 33 chia x dư 3 và 101 chia x dư 11
3)Cho biểu thức A=2017+20172+20173+...+20172018
chứng minh rằng A chia hết cho 2018
(trả lời nhanh nhất nhé mn)
1/6+3x+2=87
3x+2=87-6
3x+2=81
3x+2=34
x+2=4
x =4-2
x =2
2/
(33-3)chia hết cho x =>30 chia hết cho x
(101-11)chia hết cho x 90 chia hết cho x
x thuộc ƯC(30,90)
30=2.3.5
90=2.3.3.5
ƯCLN(30,90)=2.3.5=30
x thuộc ƯC(30,90)=Ư(30)=1 ,2,3,5,6,10,15,30
Sau khi loại các số không hợp điều kiện ta được các số:15,30
Vậy x = 15,30
3/A=2017+20172+20173+.........+20172018
A=(2017+20172)+(20173+20174)+.......(20172017+20172018)
A=2017.(1+2017)+20173.(1+2017)+..........20172017.(1+2017)
A=2017.2018+20173.2018+..................20172017.2018
=>A chia hết cho 2018
Đúng 0
Bình luận (0)
ngu the con bay dat hoi voi chang hang qua ngu qua ngu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm GTNN của P = |x - 2017| + |x- 2018|. Với x là số tự nhiên
ta có P = |2017 - x| + |x - 2018| ≥ |2017 - x + x - 2018| = 1
dấu ''='' xảy ra khi và chỉ khi 2017 ≤ x ≤ 2018
Đúng 0
Bình luận (4)
Ta có: |x-2017|+|x-2018| = |x-2017|+|2018-x| Vì: |x-2017| ≥ x-2017 (1) |2018-x| ≥ 2018-x (2) Từ (1) và (2) ⇒ |x-2017|+|2018-x| ≥ (x-2017) + (2018-x) ⇒ |x-2017|+|2018-x| ≥ 1 ⇒ P ≥ 1 Dấu "=" xảy ra khi và chỉ khi dấu "=" đồng thời xảy ra. Tức là: ⇔ |x-2017| ≥ 0 và |2018-x| ≥ 0 ⇔ x-2017 ≥ 0 và 2018-x ≥ 0 ⇔ x ≥ 2017 và x ≤ 2018 ⇔ 2017 ≤ x ≤ 2018 Mà x ∈ N nên ko có giá trị của x thỏa mãn
Đúng 0
Bình luận (3)