Giả sử x0 là nghiệm của pt x2+mx+n=0 và m2 + n2=2017 . Chứng minh |x0| < \(\sqrt{2018}\)

Những câu hỏi liên quan
Giả sử a;b là hai nghiệm của phương trình x 2 + mx + 1=0 và b;c là hai nghiệm của phương trình x 2 + nx + 2=0. Chứng minh hệ thức: (b-a)(b-c)=m.n-6.
Vì a, b là 2 nghiệm của phương trình x 2 + mx + 1 = 0 nên theo định lí Vi-et ta có:
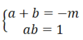
Vì b,c là 2 nghiệm của phương trình x 2 + nx + 2 = 0 nên theo định lí Vi-et ta có:
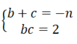
Khi đó:
(b – a)(b – c) = b 2 – bc – ab + ac
= b 2 + bc + ab + ac – 2(ab + bc)
= b( b + c) + a (b + c) – 2 (ab + bc)
= (b + c )( b + a) – 2 (ab + bc)
= (-n).(-m) – 2(1 + 2)
= nm – 6
Đúng 0
Bình luận (0)
giả sử a,b là 2 nghiệm của phương trình: x^2 + mx +1 =0 và b,c là 2 nghiệm của pt: x^2 + nx + 2 =0.
Chứng minh: (b-a)(b-c)=mn-6
Theo hệ thức Vi - ét
=> a+ b = - m và a.b = 1
b + c= - n và b.c = 2
Ta có : m .n = (-m). (-n) = (a+b). (b +c)
= [(b - a) + 2a)]. [(b- c) + 2c)] = (b - a).( b - c) + 2c( b - a) + 2a.( b - c) + 4ac
= (b - a).( b - c) + 2bc - 2ac + 2ab - 2ac + 4ac
= (b - a).( b - c) + 2.2 + 2.1 = (b - a).( b - c) + 6
=> (b - a).( b - c) =m.n - 6 (ĐPCM)
Đúng 0
Bình luận (0)
Giả sử phương trình x^2+mx+n+1=0 có các nghiệm x1,x2 là các số nguyên khác 0. Chứng minh m^2 +n^2 là 1 hợp số
Giả sử phương trình x^2 +mx+n+1=0 có các nghiệm x1,x2 là các số nguyên khác 0. Chứng minh rằng m^2 +n^2 là 1 hợp số
Giup minh vs: https://olm.vn/hoi-dap/question/1269512.html
Đúng 0
Bình luận (0)
Cho phương trình
A
x
3
+
2
C
x
+
1
x
-
1
-
3
C
x
-
1
x...
Đọc tiếp
Cho phương trình A x 3 + 2 C x + 1 x - 1 - 3 C x - 1 x - 3 = 3 x 2 + P 6 + 159 Giả sử x = x0 là nghiệm của phương trình trên, lúc này ta có
A. x0 ∈(10;13)
B. x0 ∈(12;14)
C. x0 ∈(10;12)
D. x0 ∈(14;16).
Điều kiện x ≥ 3, x ∈ N. Phương trình đã cho có dạng:
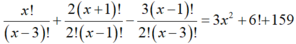
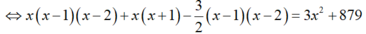
Suy ra x=12.
Chọn B.
Đúng 0
Bình luận (0)
Giả sử x0 là nghiệm của phương trình:
x2 + mx + n = 0 và m2 + n2 = 2017
Chứng minh rằng : | x0 | < \(\sqrt{2018}\)
Do x0 là một nghiệm của phương trình nên \(x_0^2+mx_0+n=0\Rightarrow n=-mx_0-x_0^2\)
Thế vào phương trình (2) ta có: \(m^2+\left(-mx_0-x_0^2\right)^2=2017\)
\(\Rightarrow m^2+m^2x_0^2+2mx_0^3+x_0^4-2017=0\)
\(\Rightarrow\left(1+x_0^2\right)m^2+2x_0^3m+\left(x_0^4-2017\right)=0\left(1\right)\)
Để pt (1) có nghiệm thì \(\Delta'\ge0\Rightarrow\left(x_0^3\right)^2-\left(1+x_0^2\right)\left(x_0^4-2017\right)\ge0\)
\(\Rightarrow-x_0^4+2017x_0^2+2017\ge0\)
\(\Rightarrow0\le x_0^2< 2018\Rightarrow\left|x_0\right|< \sqrt{2018}\left(đpcm\right)\)
Đúng 1
Bình luận (0)
Cho pt x^2-mx-1=0 a) chứng minh pt có 2 nghiệm trái dấu b) gọi x1,x2 là các nghiệm của pt 1 Tính giá trị của biểu thức P= x1^2+x1-1/x1 - x2^2+x2-1/x2
1. cho pt x2-2(m-2)x-2m0 với x là ẩn số giá trị của m để pt có 2 nghiệm là 2 số đối nhau là a,0 b, dfrac{-1}{2} c, 2 d, 4 2. biết rằng (x0; y0)là nghiệm của hệ pt left{{}begin{matrix}x+2y-302x-y-10end{matrix}right. tổng x0 + y0 bằng a,3 b,1 c,0 d, 23. trong △ABC vuông tại A có AC3; AB4 khi đó tanB bằng a,dfrac{4}{5} b,dfrac{3}{5} c,dfrac{3}{4} d dfrac{4}{3}4. trên đg tròn (O;R) lấy 2 điểm A,B sao cho số đo cung AB lớn hơn...
Đọc tiếp
1. cho pt x2-2(m-2)x-2m=0 với x là ẩn số giá trị của m để pt có 2 nghiệm là 2 số đối nhau là
a,0 b, \(\dfrac{-1}{2}\) c, 2 d, 4
2. biết rằng (x0; y0)là nghiệm của hệ pt \(\left\{{}\begin{matrix}x+2y-3=0\\2x-y-1=0\end{matrix}\right.\) tổng x0 + y0 bằng
a,3 b,1 c,0 d, 2
3. trong △ABC vuông tại A có AC=3; AB=4 khi đó tanB bằng
a,\(\dfrac{4}{5}\) b,\(\dfrac{3}{5}\) c,\(\dfrac{3}{4}\) d \(\dfrac{4}{3}\)
4. trên đg tròn (O;R) lấy 2 điểm A,B sao cho số đo cung AB lớn hơn bằng \(270^o\) độ dài dây cung là
a, R\(\sqrt{2}\) b, R\(\sqrt{3}\) c, R d, 2R\(\sqrt{2}\)
5. cho đg tròn (O;3cm) 2 điểm A,B thuộc đường tròn và sđ \(\stackrel\frown{AB}\) = \(60^o\) độ dài cung nhỏ AB là
a, \(\dfrac{\pi}{2}\) cm b, \(3\pi\) c, \(\dfrac{\pi}{3}cm\) d, \(\pi\)cm
6. giá trị của m để 2 đg thẳng (d): y=xm+6 và (d'): y=3x+2-m song song là
a, m=-2 b, m=-3 c, m=-4 d, m=1
7. cho hàm số bậc nhất y=ax+b có hệ số góc bằng -1 và tung độ góc bằng 3 giá trị của biểu thức a2+b bằng
a,2 b, 4 c, 9 d, 5
8. cho hệ pt \(\left\{{}\begin{matrix}3x+my=1\\nx+y=3\end{matrix}\right.\) với m,n là tham số biết rằng (x;y)=(1,1) là 1 nghiệm của hệ đã cho giá trị của m+n bằng
a, -1 b, 3 c, 1 d, 2
9.cho Parabol (P) có pt \(y=\dfrac{x^2}{4}\) vào đường thẳng (d): y=-2x-4
a, (P) cắt (d) tại 2 điểm phân biệt
b, (P) cắt (d) tại điểm duy nhất (-2;2)
c, (P) ko cắt (d)
d, (P) tiếp xúc với (d), tiếp điểm là (-4;4)
10. tất cả các giá trị của x để \(\sqrt{-2x+6}\) có nghĩa là
a, x≥3 b, x>3 c, x≤3 d, x<-3
Câu 3: C
Câu 4: A
Câu 5: C
Câu 6: m=3
Câu 7: B
Câu 8: D
Câu 9: D
Câu 10: C
Đúng 1
Bình luận (0)
Chứng minh rằng phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 thỏa mãn 0 < x 0 < 1 2
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].

- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
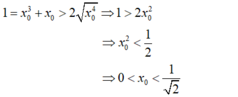
Đúng 0
Bình luận (0)















