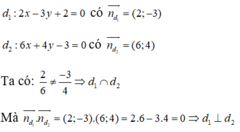xác định vị trí tương đối giữa hai đường thảng delta1: x-2y+1=0 và delta2: -3x+6y-10=0

Những câu hỏi liên quan
xác định vị trí tương đối của 2 đường thẳng sau đây △1: x-2y+1=0; △2: -3x+6y-10=0
Xác định vị trí tương đối của 2 đường thẳng sau đây: (d1): x- 2y+ 10 và (d2): -3x+ 6y-1 0 . A. Song song. B. Trùng nhau. C. Vuông góc nhau. D. Cắt nhau.
Đọc tiếp
Xác định vị trí tương đối của 2 đường thẳng sau đây: (d1): x- 2y+ 1=0 và (d2): -3x+ 6y-1 =0 .
A. Song song.
B. Trùng nhau.
C. Vuông góc nhau.
D. Cắt nhau.
Đường thẳng (d1) có vtpt ![]() và
và
d2 có vtpt ![]()
Hai đường thẳng này có
![]() nên hai đường thẳng này song song với nhau.
nên hai đường thẳng này song song với nhau.
Chọn A.
Đúng 0
Bình luận (0)
Câu 1: Viết phương trình tham số, phương trình tổng quát của đường thẳng đi qua hai điểm A(4;1) và B(4;2)
Câu 2: Xét vị trí tương đối của cặp đường thẳng sau:
Delta1:left{{}begin{matrix}x5+iy-3+2iend{matrix}right.và Delta2:3x-2y-260
Câu 3: Tính khoảng cách từ điểm M(2;3) đến đường thẳng Delta:3x-4y+40
Câu 4: Tìm góc giữa hai đường thẳng Delta1:x+2y+40 và Delta2:2x-y+60
mọi người đọc qua và giải giúp mình vs cảm ơn rất nhiều
Đọc tiếp
Câu 1: Viết phương trình tham số, phương trình tổng quát của đường thẳng đi qua hai điểm A(4;1) và B(4;2)
Câu 2: Xét vị trí tương đối của cặp đường thẳng sau:
\(\Delta1:\left\{{}\begin{matrix}x=5+i\\y=-3+2i\end{matrix}\right.\)và \(\Delta2:3x-2y-26=0\)
Câu 3: Tính khoảng cách từ điểm M(2;3) đến đường thẳng \(\Delta:3x-4y+4=0\)
Câu 4: Tìm góc giữa hai đường thẳng \(\Delta1:x+2y+4=0\) và \(\Delta2:2x-y+6=0\)
mọi người đọc qua và giải giúp mình vs cảm ơn rất nhiều
a/ \(\overrightarrow{AB}=\left(0;1\right)\Rightarrow\) đường thẳng AB có 1 vtpt là \(\overrightarrow{n_{AB}}=\left(1;0\right)\) và 1 vtcp là \(\overrightarrow{u_{AB}}=\left(0;1\right)\)
- Phương trình tham số AB: \(\left\{{}\begin{matrix}x=4+0.t\\y=1+1.t\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=1+t\end{matrix}\right.\)
- Phương trình tổng quát:
\(1\left(x-4\right)+0\left(y-1\right)=0\Leftrightarrow x-4=0\)
b/ Thay tọa độ x; y từ \(\Delta_1\) vào \(\Delta_2\) ta được:
\(3\left(5+i\right)-2\left(-3+2i\right)-26=0\)
\(\Leftrightarrow-i-5=0\Rightarrow i=-5\)
Thay \(i=-5\) vào pt \(\Delta_1\Rightarrow\left\{{}\begin{matrix}x=5-5=0\\y=-3+2.\left(-5\right)=-13\end{matrix}\right.\)
\(\Rightarrow\Delta_1\) cắt \(\Delta_2\) tại điểm có tọa độ \(\left(0;-13\right)\)
c/ Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|3.2-4.3+4\right|}{\sqrt{3^2+\left(-4\right)^2}}=\frac{2}{5}\)
d/ Ta có \(\overrightarrow{n_{\Delta1}}=\left(1;2\right)\) và \(\overrightarrow{n_{\Delta2}}=\left(2;-1\right)\)
\(\Rightarrow\overrightarrow{n_{\Delta1}}.\overrightarrow{n_{\Delta2}}=1.2+2.\left(-1\right)=2-2=0\)
\(\Rightarrow\Delta_1\perp\Delta_2\) hay góc giữa \(\Delta_1\) và \(\Delta_2\) bằng \(90^0\)
Đúng 0
Bình luận (1)
xác định vị trí tương đối giữa 2 đường thẳng delta 1: x-2x+1=0 và delta 2: -3x-4y-1=0
Xem lại đề phương trình đường thẳng delta1
Đúng 0
Bình luận (0)
Xác định vị trí tương đối của 2 đường thẳng sau đây:
△1: x-2y+1=0; △2: -3x+6y-10=0
Phương trình tọa độ giao điểm:
\(\left\{{}\begin{matrix}x-2y+1=0\\-3x+6y-10=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-6y+3=0\\-3x+6y-10=0\end{matrix}\right.\)
Cộng vế với vế: \(-7=0\) (vô nghiệm)
Vậy 2 đường thẳng đã cho song song
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
Xét Δ và d1, hệ phương trình: 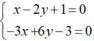 có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: 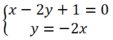 có nghiệm duy nhất (-1/5; 2/5) nên
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: 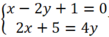 vô nghiệm
vô nghiệm
Vậy Δ // d3
Đúng 0
Bình luận (0)
Xét vị trí tương đối của hai đường thẳng
d
1
:
3
x
−
2
y
−
6
0
và
d
2
:
6
x
−
2
y
−
8
0
A. Trùng nhau. B. Song song. C. Vuông góc với nhau. D. Cắt nhau nhưng không vuông góc nhau.
Đọc tiếp
Xét vị trí tương đối của hai đường thẳng d 1 : 3 x − 2 y − 6 = 0 và d 2 : 6 x − 2 y − 8 = 0
A. Trùng nhau.
B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Xét vị trí tương đối của mỗi cặp đường thẳng sau
a) \({d_1}:3x + 2y--5 = 0\) và \({d_2}:x - 4y + 1 = 0\) ;
b) \({d_3}:x - 2y + 3 = 0\) và \({d_4}: - {\rm{ }}2x + 4y + 10 = 0\) ;
c) \({d_5}:4x + 2y - 3 = 0\) và \({d_6}:\left\{ \begin{array}{l}x = - \frac{1}{2} + t\\y = \frac{5}{2} - 2t\end{array} \right.\)
a) Tọa độ giao điểm của hai đường thẳng \({d_1},{d_2}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}3x + 2y - 5 = 0\\x - 4y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{9}{7}\\y = \frac{4}{7}\end{array} \right.\)
Hệ phương trình có nghiệm duy nhất nên 2 đường thẳng cắt nhau.
b) Tọa độ giao điểm của hai đường thẳng \({d_3},{d_4}\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - 2y + 3 = 0\\ - 2x + 4y + 10 = 0\end{array} \right.\) .
Hệ phương trình vô nghiệm.nên 2 đường thẳng song song với nhau
c) Tọa độ giao điểm của hai đường thẳng \({d_5},{d_6}\) tương ứng với t thỏa mãn phương trình:
\(4\left( { - \frac{1}{2} + t} \right) + 2\left( {\frac{5}{2} - 2t} \right) - 3 = 0 \Leftrightarrow 0t = 0\) .
Phương trình này có nghiệm với mọi t. Do đó \({d_5} \equiv {d_6}\).
Đúng 0
Bình luận (0)
Xác định vị trí tương đối của hai đường thẳng d1: 2x - 3y + 2 = 0 và d2: 6x + 4y - 3 = 0
A. Song song
B. vuông góc
C. trùng nhau
D. cắt nhưng không vuông