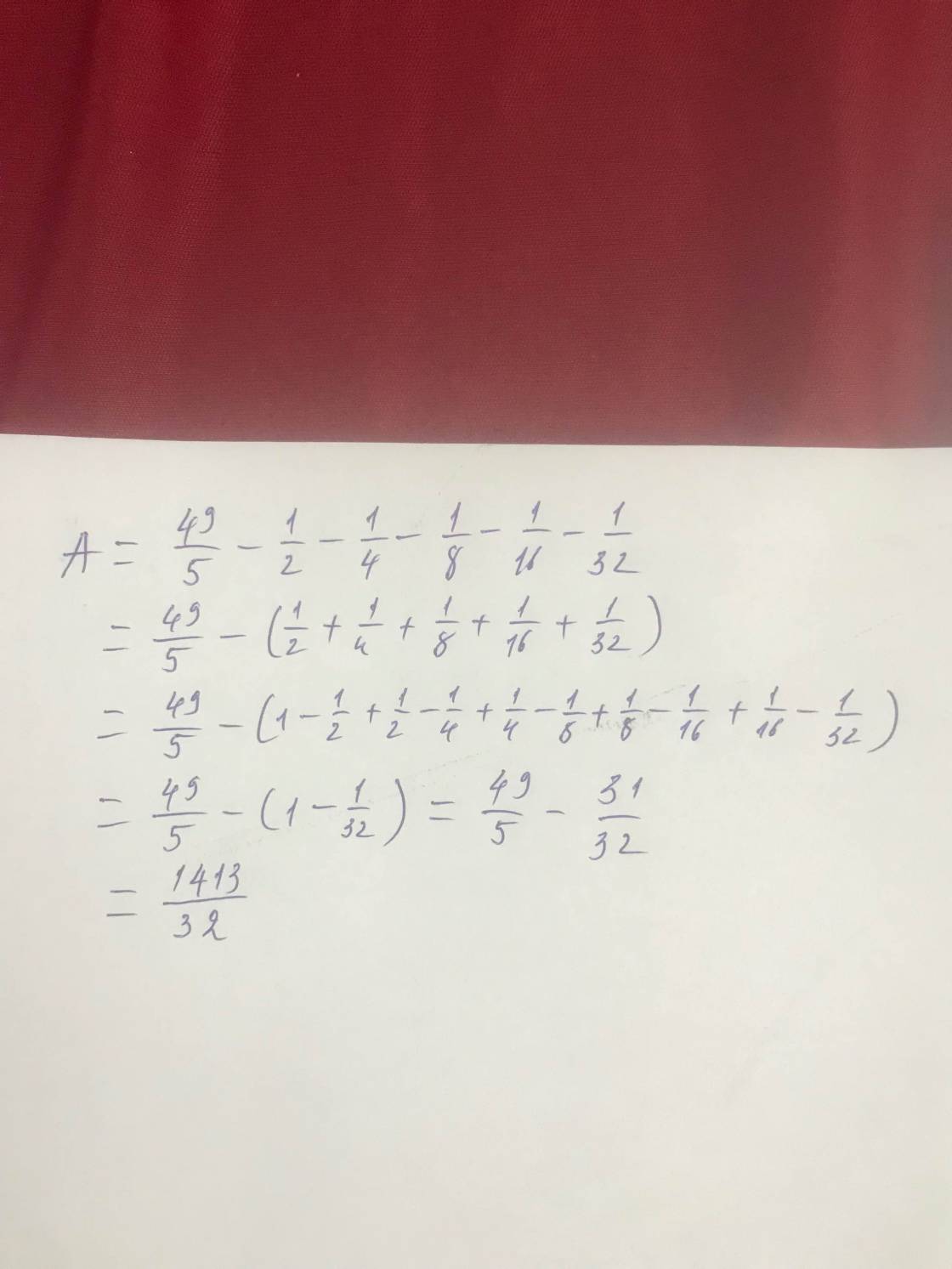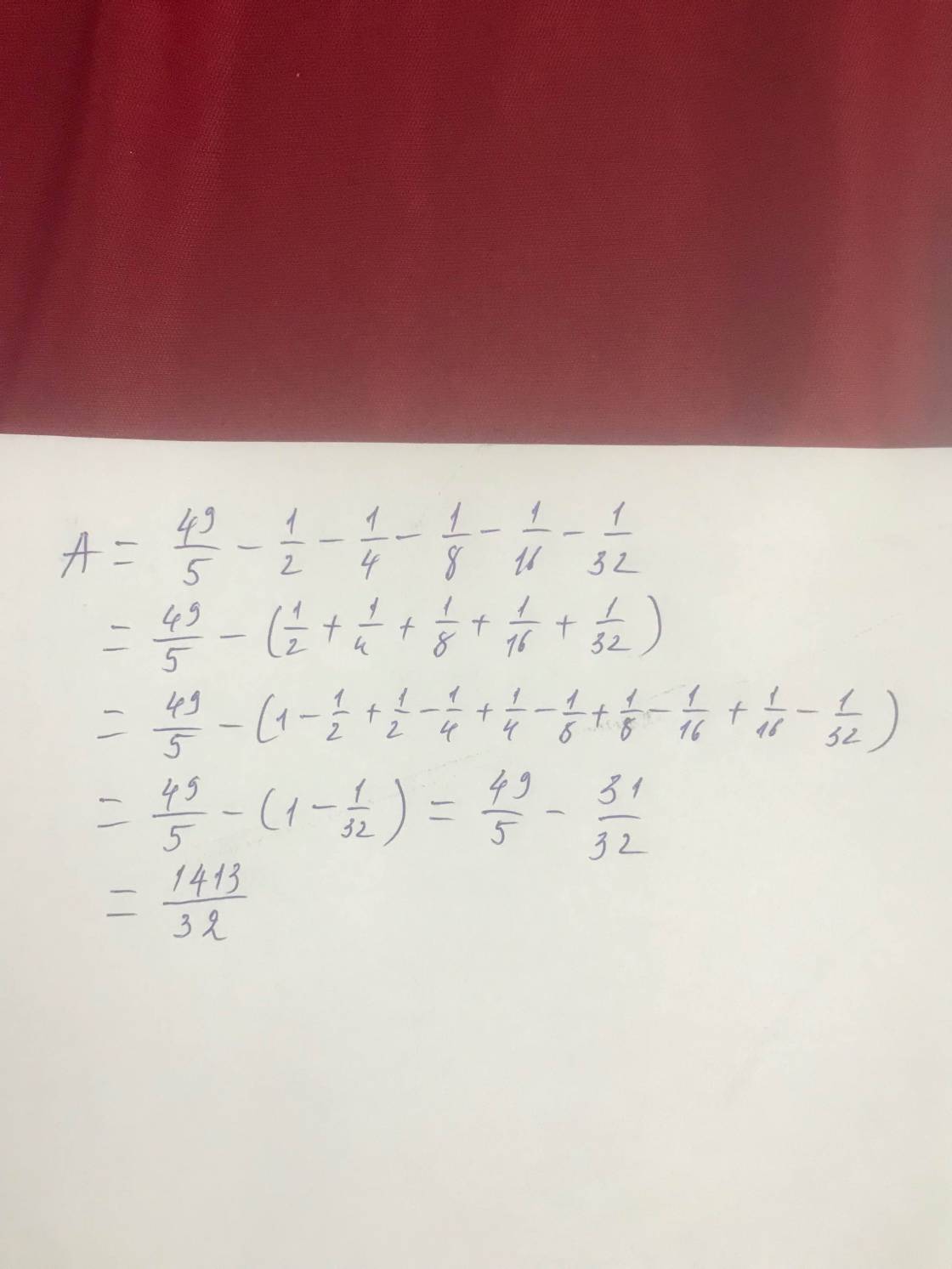Nhanh lên giúp tớ

1413/160

49/5 + 1/2 - 1/4 - 1/8 - 1/16 - 1/32 = 1413/60 = 8,83125

1573/160 tính mệt ghê

1573/160

\(A=\dfrac{49}{5}-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}\right)\)

\(A=\dfrac{49}{5}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{32}\right)\)

\(A=\dfrac{49}{5}-\left(1-\dfrac{1}{32}\right)=\text{​​}\dfrac{49}{5}-\dfrac{31}{32}\text{​​}\)

\(A=\dfrac{1413}{160}\text{​​}\)

Ta có : \(\frac{49}{5}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}\)

\(=\frac{49}{5}-\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\right)\)

Đặt \(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}\)

=> \(2A=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\)

=> \(2A-A=1-\frac{1}{32}\Rightarrow A=\frac{31}{32}\)

Vậy \(\frac{49}{5}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}\)

\(=\frac{49}{5}-\frac{31}{32}=\frac{1413}{160}\)

\(\frac{49}{5}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}\)\(=\)\(\frac{4189}{480}\)

6:=(3/2)*(3/2)^2*(3/2)^4=(3/2)^7

7: =(1/2)^7*2^3*2^5*2^8=2^9

8: =(-1/7)^4*5^4=(-5/7)^4

9: =2^2*2^5:(2^3/2^4)

=2^7/2=2^6

10: =(1/7)^3*7^2=1/7

\(\dfrac{3}{2}\times\dfrac{9}{4}\times\dfrac{81}{16}=\dfrac{3}{2}\times\left(\dfrac{3}{2}\right)^2\times\left(\dfrac{3}{2}\right)^4=\left(\dfrac{3}{2}\right)^7\)

\(\left(\dfrac{1}{2}\right)^7\times8\times32\times2^8=\left(\dfrac{1}{2}\right)^7\times2^3\times2^5\times2^8=\left(\dfrac{1}{7}\right)^7\times2^{16}\)

\(\left(-\dfrac{1}{7}\right)^4\times125\times5=\left(-\dfrac{1}{7}\right)^4\times5^3\times5=\left(-\dfrac{1}{7}\right)^4\times5^4\)

\(4\times32:\left(2^3\times\dfrac{1}{16}\right)=2^2\times2^5:2^3:2^{-4}=2^0\)

\(\left(\dfrac{1}{7}\right)^2\times\dfrac{1}{7}\times49=\left(\dfrac{1}{7}\right)^3\times7^3=1^3\)
 

6, \(\dfrac{3}{2}\times\dfrac{9}{4}\times\dfrac{81}{16}=\dfrac{3}{2}\times\left(\dfrac{3}{2}\right)^2\times\left(\dfrac{3}{2}\right)^4\)

7,\(\left(\dfrac{1}{2}\right)^7\times8\times32\times2^8=\left(\dfrac{1}{2}\right)^7\times2^3\times2^5\times2^8\)

8,\(\left(-\dfrac{1}{7}\right) ^4\times125\times5=\left(\dfrac{1}{7}\right)^4\times5^3\times5\)

9,\(4\times32:\left(2^3\times\dfrac{1}{16}\right)=2^2\times2^5:\left[2^3\times\left(\dfrac{1}{2}\right)^4\right]\)

10, \(\left(\dfrac{1}{7}\right)^2\times\dfrac{1}{7}\times49=\left(\dfrac{1}{7}\right)^2\times\dfrac{1}{7}\times7^2\)

6) \(...=\dfrac{3}{2}.\left(\dfrac{3}{2}\right)^2.\left(\dfrac{3}{2}\right)^4=\left(\dfrac{3}{2}\right)^7\)

7) \(...=2^{-7}.2^3.2^5.2^8=2^9\)

8) \(...=\left(\dfrac{1}{7}\right)^4.5^3.5=\left(\dfrac{1}{7}\right)^4.5^4\)

9) \(...=2^2.2^5:\left(2^3.2^{-4}\right)=2^8\)

10) \(...=\left(\dfrac{1}{7}\right)^3.\left(\dfrac{1}{7}\right)^2=\left(\dfrac{1}{7}\right)^5\)

tính nhanh 

49/5-1/2-1/4-1/8-1/16-1/32=8,83125

nha bn duyệt đi

\(\frac{49}{5}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}=\frac{1413}{160}=8,83125\)

a) Số các số hạng là:

( 99-49):2+1​\(=\)​26 ( số )

Tổng của dãy số trên là:

 ( 99 + 49 ) x 26 : 2 \(=\)1924

Đáp số: 1924

b) \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)

\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{8}+\frac{1}{8}-\frac{1}{16}+\frac{1}{16}-\frac{1}{32}+\frac{1}{32}-\frac{1}{64}+\frac{1}{64}-\frac{1}{128}\)

\(=\frac{1}{1}-\frac{1}{128}\)

\(=\frac{127}{128}\)

a) Số các số hạng là (99 - 49) : 2 + 1 = 26 số

Tổng của dãy trên là:

(99 + 49) x 26 : 2 = 1924

Đáp số : 1924

b) 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128

= 1/1 - 1/2 + 1/2 - 1/4 + 1/4 - 1/8 + 1/8 - 1/16 + 1/16 - 1/32 + 1/32 - 1/64 + 1/64 - 1/128

= 1/1 - 1/128

= 127/128

a) GIẢI:

Số số hạng dãy số là:

(99-49):2+1=26

Tổng dãy số là:

(49+99)x26:2=1924

Vậy tổng dãy số là 1924

Đáp số : 1924