Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Biết DN=18cm,AH=22cm

Những câu hỏi liên quan
Cho hình bình hành ABCD có M và N là trung điểm của AB và CD . biết DN = 28cm , AH = 3dm . tính tổng diện tích của hình bình hành
cho hình bình hành ABCD có M và N là trung điểm của AB và CD . Biết DN = 18 cm , AH=22 cm . Tính tổng diện tích của các hình bình hành có trong hình
(có nhiều cách giải)
Hình bên có tất cả 3 hình nình hành gồm AMND, MBCN và ABCD
Vì M và N là trung điểm của AB và CD nên AM = MB = DN = Nc = 18 cm
Diện tích hình bình hành AMND là : 22 x 18 = 369 (cm2)
Tổng diện tích các hình bình hành có trong hình vẽ chính bằng tổng diện tích của 4 hình bình hành AMND là : 396 x 4 = 1584 cm2
Đáp số : 1584 cm2
Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Biết DN = 18 cm, AH = 22 cm (như hình vẽ ): Tính tổng diện tích của các hình bình hành có trong hình vẽ :
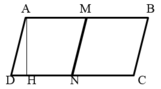
(có nhiều cách giải)
Hình bên có tất cả 3 hình nình hành gồm AMND, MBCN và ABCD
Vì M và N là trung điểm của AB và CD nên AM = MB = DN = Nc = 18 cm
Diện tích hình bình hành AMND là : 22 x 18 = 369 (cm2)
Tổng diện tích các hình bình hành có trong hình vẽ chính bằng tổng diện tích của 4 hình bình hành AMND là : 396 x 4 = 1584 cm2
Đáp số : 1584 cm2
Đúng 1
Bình luận (2)
cao minh tâm ơi Diện tích hình bình hành AMND là : 22 x 18 = 369 (cm2)sai rồi =396 mà
Đúng 0
Bình luận (0)
*c.Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Biết DN = 18 cm, AH = 22 cm (như hình vẽ ). Tính tổng diện tích của các hình bình hành có trong hình vẽ:……………………………………………...

Cho hình bình hành ABCD. Gọi M, N là trung điểm của AB, CD. CM và AN cắt BD tại P, Q. Biết BD = 18cm. Tính PQ.
bạn dùng tính chất của đg trung bình là ra
Đúng 0
Bình luận (0)
M là trung điểm \(AB\Rightarrow AM=0,5AB\)
N là trung điểm \(CD\Rightarrow CN=0,5CD\)
Mà \(AB=CD\) ( tính chất hình bình hành ) \(\Rightarrow AM=CN\)
Xét tứ giác AMCN có cặp cạnh đối AM , CN song song và bằng nhau nên AMCN là hình bình hành .
\(\Rightarrow CM||AN\Rightarrow QN||\)| PC VÀ PM | ||AQ
Áp dụng định lí Ta - let cho các cặp cạnh song song trên ta có :
\(\frac{DQ}{QP}=\frac{DN}{NC}=1\Rightarrow DQ=QP\left(1\right)\)
\(\frac{BP}{PQ}=\frac{BM}{AM}=1\Rightarrow BP=PQ\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow DQ=QP=BP\)
Mà \(DQ+PQ+BP=BD=18\left(cm\right)\)
\(\Rightarrow PQ=\frac{BD}{3}=6\left(cm\right)\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có CD=4cm, đường cao vẽ từ AH đến cạnh CD bằng 3cm.
a, Tính diện tích nình bình hành ABCD.
b, Gọi M là trung điểm của AB. Tính diện tích △ADM.
c, DM cắt AC tại N. Chứng minh DN=2NM.
d, Tính diện tích △AMN.
Cho hình bình hành ABCD có CD=4cm, đường cao vẽ từ AH đến cạnh CD bằng 3cm.
a, Tính diện tích nình bình hành ABCD.
b, Gọi M là trung điểm của AB. Tính diện tích △ADM.
c, DM cắt AC tại N. Chứng minh DN=2NM.
d, Tính diện tích △AMN.
a, \(S_{ABCD}\) = AH.CD
= 3.4
= 12 (\(cm^2\))
b, Ta có M là trung điểm AB
⇒ AM = \(\dfrac{AB}{2}\) = \(\dfrac{4}{2}\) = 2 (cm)
\(S_{ADM}\) = \(\dfrac{AH.AM}{2}\)
= \(\dfrac{3.2}{2}\)
= 3 (\(cm^2\))
c, Gọi O là trung điểm
Đúng 1
Bình luận (0)
c, Gọi O là trung điểm ND
Từ O kẻ OP // CD
Xét ΔNDC có: NO = OD
OP // CD
⇒ OP là đường trung bình ΔNDC
⇒ OP = \(\dfrac{1}{2}DC\) mà DC = 4 cm
⇒ OP = 2 cm
Xét ΔAMN và ΔPON có:
Góc BAC = góc APO
Góc MOP = góc AMD
AM = ON
⇒ ΔAMN = ΔPON (g.c.g)
⇒ NM = ON mà ON = \(\dfrac{1}{2}DM\)
⇒ DN = 2MN
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có AB // CD, DC = 2AB, AD vuông góc AB. Kẻ AH vuông góc AC tại H, M tương ứng là trung điểm của HD và HC, AM cắt DN tại K, E là trung điểm của DC
1. Chứng minh ABNM là hình bình hành
2. Chứng minh M là trực tâm của tam giác DAN
3. Chứng minh BN vuông góc với ND và MN đi qua trung điểm của HE
Giúp mình nha, thanks nhìu ^^
Sửa đề: DH vuông góc AC
1: Xét ΔHDC có
M,N lần lượt là trung điểm của HD,HC
nên MN là đường trung bình
=>MN//DC và MN=DC/2
=>MN//AB và MN=AB
=>ABNM là hình bình hành
2: NM//AB
=>NM vuông góc AD
Xét ΔAND có
DH,NM là các đường cao
DH cắt NM tại M
=>M là trực tâm
3: Xét ΔHDC có
E,N lần lượt là trung điểm của CD,CH
nên EN là đường trung bình
=>EN//HD và EN=HD/2
=>EN//HM và EN=HM
=>HMEN là hình bình hành
=>MN đi qua trung điểm của HE
Đúng 1
Bình luận (2)
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM=DN. Đường trung trực của BM lần lượt cắt các đương thẳng MN và BC tại E và F. Hình bình hành ABCD phải có thêm điều kiện gì để tứ giác BCNE là hình thang cân?



















