Ta có

2 ⋅ P ( x ) = 2 ⋅ − 6 x 5 − 4 x 4 + 3 x 2 − 2 x = − 12 x 5 − 8 x 4 + 6 x 2 − 4 x  Khi dó  2 P ( x ) + Q ( x ) = − 12 x 5 − 8 x 4 + 6 x 2 − 4 x + 2 x 5 − 4 x 4 − 2 x 3 + 2 x 2 − x − 3

= - 12 x 5 - 8 x 4 + 6 x 2 - 4 x + 2 x 5 - 4 x 4 - 2 x 3 + 2 x 2 - x - 3 = - 12 x 5 + 2 x 5 + - 8 x 4 - 4 x 4 - 2 x 3 + 6 x 2 + 2 x 2 + ( - 4 x - x ) - 3 = - 10 x 5 - 12 x 4 - 2 x 3 + 8 x 2 - 5 x - 3

Chọn đáp án B

Ta có

M ( x ) = P ( x ) − Q ( x ) = − 6 x 5 − 4 x 4 + 3 x 2 − 2 x − 2 x 5 − 4 x 4 − 2 x 3 + 2 x 2 − x − 3 = − 8 x 5 + 2 x 3 + x 2 − x + 3  Có  M ( − 1 ) = − 8. ( − 1 ) 5 + 2 ⋅ ( − 1 ) 3 + ( − 1 ) 2 − ( − 1 ) + 3 = 11

Chọn đáp án A

bạn để câu hỏi thế thì ai biết mà giúp

`@` `\text {Ans}`

`\downarrow`

`a)`

Thu gọn:

`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)

`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`

`= -x^5 + 5x^4 + 2x^2 + 2x - 4`

`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)

`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`

`= x^5 - x^4 - x^3 - x^2 + 7x - 2`

`@` Tổng:

`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)

`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`

`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`

`= 4x^4 - x^3 + x^2 + 9x - 6`

`@` Hiệu:

`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)

`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`

`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`

`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`

`b)`

`@` Thu gọn:

\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)

`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`

`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`

`= x^4 - 2x^3 - x^2 + 15x + 10`

\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)

`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`

`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`

`= x^4 + 3x^3 + 2x - 4`

`@` Tổng:

`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)

`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`

`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`

`= 2x^4 + x^3 - x^2 + 17x + 6`

`@` Hiệu: 

`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)

`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`

`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`

`= -5x^3 - x^2 + 13x + 14`

`@` `\text {# Kaizuu lv u.}`

a) \(\left(2x^3-x^2+5x\right):x\)

\(=\dfrac{2x^3-x^2+5x}{x}\)

\(=\dfrac{x\left(2x^2-x+5\right)}{x}\)

\(=2x^2-x+5\)

b) \(\left(3x^4-2x^3+x^2\right):\left(-2x\right)\)

\(=\dfrac{3x^4-2x^3+x^2}{-2x}\)

\(=\dfrac{2x\left(\dfrac{3}{2}x^3-x^2+\dfrac{1}{2}x\right)}{-2x}\)

\(=-\left(\dfrac{3}{2}x^3-x^2+\dfrac{1}{2}x\right)\)

\(=-\dfrac{3}{2}x^3+x^2-\dfrac{1}{2}x\)

c) \(\left(-2x^5+3x^2-4x^3\right):2x^2\)

\(=\dfrac{-2x^5+3x^2-4x^3}{2x^2}\)

\(=\dfrac{2x^2\left(-x^3+\dfrac{3}{2}-2x\right)}{2x^2}\)

\(=-x^3-2x+\dfrac{3}{2}\)

d) \(\left(x^3-2x^2y+3xy^2\right):\left(-\dfrac{1}{2}x\right)\)

\(=\dfrac{x^3-2x^2y+3xy^2}{-\dfrac{1}{2}x}\)

\(=\dfrac{\dfrac{1}{2}x\left(2x^2-4xy+6y^2\right)}{-\dfrac{1}{2}x}\)

\(=-\left(2x^2-4xy+6y^2\right)\)

\(=-2x^2+4xy-6y^2\)

e) \(\left[3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2\right]:5\left(x-y\right)^2\)

\(=\dfrac{3\left(x-y\right)^5-2\left(x-y\right)^4+3\left(x-y\right)^2}{5\left(x-y\right)^2}\)

\(=\dfrac{5\left(x-y\right)^2\left[\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\right]}{5\left(x-y\right)^2}\)

\(=\dfrac{3}{5}\left(x-y\right)^3-\dfrac{2}{5}\left(x-y\right)^2+\dfrac{3}{5}\)

f) \(\left(3x^5y^2+4x^3y^3-5x^2y^4\right):2x^2y^2\)

\(=\dfrac{3x^5y^2+4x^3y^3-5x^2y^4}{2x^2y^2}\)

\(=\dfrac{2x^2y^2\left(\dfrac{3}{2}x^3+2xy-\dfrac{5}{2}y^2\right)}{2x^2y^2}\)

\(=\dfrac{3}{2}x^3+2xy-\dfrac{5}{2}y^2\)

Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có

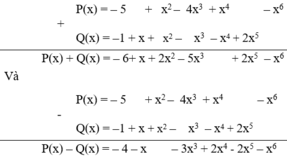
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6

P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6